ОБРАТНЫЕ МАТРИЦЫ
3.1. Определения и примеры.Для квадратной матрицы A(nxn) обратной к ней является матрица Пример 3.1. Является ли матрица Решение. Найдем произведения этих матриц:
Итак, Теорема о существовании. Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля (т.е. когда матрица является невырожденной). 3.2. Поиск обратной матрицы с помощью метода Гаусса. После вычисления определителя (чтобы убедиться, что обратная матрица существует) необходимо выписать матрицу, приписать к ней справа единичную соответствующего размера и «сдвоенную» матрицу Пример 3.2. Найти Решение. матрица
Таким образом, 3.3. Поиск обратной матрицы с помощью алгебраических дополнений к элементам исходной матрицы. Это способ основан на применении формулы
где Пример 3.3. Найти Решение. Матрица та же самая, что в примере 3.2, поэтому ее определитель нам уже известен (
Итак, Замечание. Результат поиска обратной матрицы можно проверить и другим способом – убедиться в справедливости равенства Пример 3.4. Решить уравнения а) Решение. Матричное уравнение
Значит,
Замечание. Результат можно проверить, подставив полученные матрицы в исходные уравнения.
|

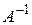 того же размера, удовлетворяющая равенствам:
того же размера, удовлетворяющая равенствам: 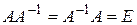 , где E – единичная матрица соответствующего размера.
, где E – единичная матрица соответствующего размера.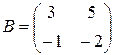 обратной к
обратной к 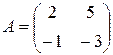 .
.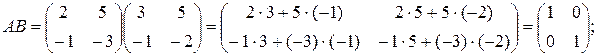
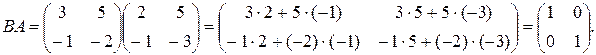 .
.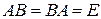 и
и  .
.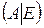 путем элементарных преобразований привести к выражению
путем элементарных преобразований привести к выражению 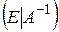 (слева должна стоять единичная матрица, а справа появится искомая обратная).
(слева должна стоять единичная матрица, а справа появится искомая обратная).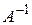 для
для 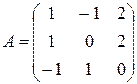 .
.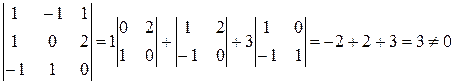 . Значит,
. Значит,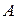 невырожденная и имеет обратную. Составим «сдвоенную» матрицу и проведем необходимые преобразования.
невырожденная и имеет обратную. Составим «сдвоенную» матрицу и проведем необходимые преобразования.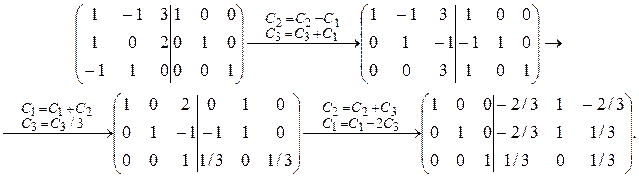
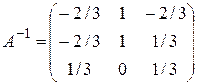 .
.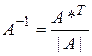 , (9)
, (9)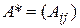 - матрица из алгебраических дополнений к элементам матрицы A.
- матрица из алгебраических дополнений к элементам матрицы A.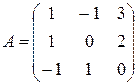 методом алгебраических дополнений.
методом алгебраических дополнений.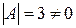 ). Найдем алгебраические дополнения к элементам исходной матрицы:
). Найдем алгебраические дополнения к элементам исходной матрицы: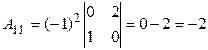 ;
;
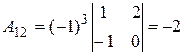 ;
;
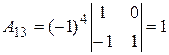 ;
;
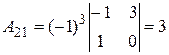 ;
;
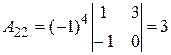 ;
;
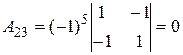 ;
;
 ;
;
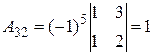 ;
;
 .
.
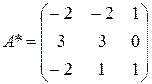 ;
; 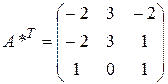 . По формуле (9) получаем:
. По формуле (9) получаем: 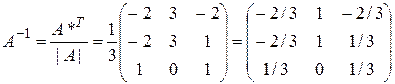 . Эта матрица совпала с найденной при решении примера 3.2, что может служить проверкой правильности решения.
. Эта матрица совпала с найденной при решении примера 3.2, что может служить проверкой правильности решения.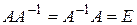 .
.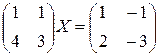 ; б)
; б) 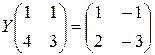 .
.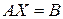 можно умножить слева на
можно умножить слева на 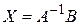 (в силу определения обратной матрицы). С другой стороны, уравнение
(в силу определения обратной матрицы). С другой стороны, уравнение 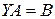 умножаем на матрицу
умножаем на матрицу 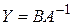 . Найдем матрицу, обратную к
. Найдем матрицу, обратную к 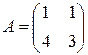 . Используя метод Гаусса, получаем:
. Используя метод Гаусса, получаем: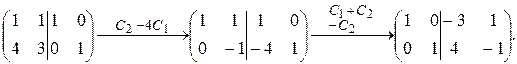
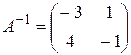 . Но тогда
. Но тогда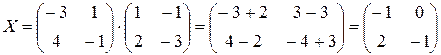 ;
;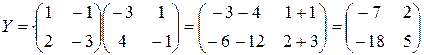 .
.


