ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ. ТЕОРЕМА КРАМЕРА
2.1. Вычисление определителей. Для определителя квадратной матрицы A(nxn) используются обозначения
Определитель матрицы A(3x3) (определитель третьего порядка) сводится к предыдущему случаю по правилу (формула раскрытия определителя по первой строке):
Минором элемента
Формула (3) обобщается на случай определителя любой квадратной матрицы A(nxn) (определителя n-го порядка):
Более того, определитель n-го порядка можно раскрывать по любой строке или любому столбцу исходной матрицы, т.е. справедливы формулы:
где i=1,2,…,n – номер строки, а j=1,2,…,n – номер столбца, по которым раскрывается определитель. Пример 2.1. Найти: а) Решение. При нахождении определителя а) воспользуемся формулой (2), а затем (для вычисления определителей 2-го порядка) формулой (1):
При вычислении определителя б) удобно применить формулу (5) для i=2, т.е. раскрыть определитель по второй строке.
Полученный на промежуточном этапе определитель 3-го порядка также будем раскрывать по второй строке:
Итак, Пример 2.2. Найти минор Решение. Минор
Далее,
Замечание. При расчетах удобно использовать свойства определителей: 1) Определитель диагональной, а также верхней (нижней) треугольной матрицы равен произведению элементов, стоящих на главной диагонали. 2) Если в матрице две строки (два столбца) меняются местами, то ее определитель меняет знак. 3) Если в строке (столбце) матрицы все элементы имеют общий множитель, то его выносят за знак определителя. 4) Если к одной из строк матрицы прибавить другую, умноженную на число (отличное от нуля), то определитель не изменится. 5) Если матрица содержит нулевую строку или равные (пропорциональные) строки, то ее определитель равен нулю. Свойства 4)-5) также справедливы и для столбцов. Пример 2.3. Вычислить а) Решение. В первой строке определителя из задания а) все числа кратны 2, поэтому общий множитель можно вынести за знак определителя. Далее проводим преобразования с целью получить в третьем столбце нулевые элементы. Вв полученном определителе 2-я и 3-я строки равны, значит, исходный определитель обратится в нуль: При вычислении определителя б) приведем матрицу к верхнему треугольному виду, учитывая свойства 3), 2), 4), а затем воспользуемся свойством 1).
2.2. Приложения определителей к решению систем линейных уравнений. Теория определителей позволяет решать "квадратные" системы линейных уравнений (в случае, когда число неизвестных совпадает с числом уравнений):
Матрица Теорема Крамера. Если определитель матрицы системы (7) отличен от нуля (
где Пример 2.4. Решить систему Решение. Выписываем A - матрицу системы и B - столбец свободных членов:
По теореме Крамера
|

 или
или  . Определитель квадратной матрицы A(2x2) (определитель второго порядка) находится по формуле:
. Определитель квадратной матрицы A(2x2) (определитель второго порядка) находится по формуле: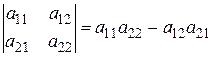 (1)
(1)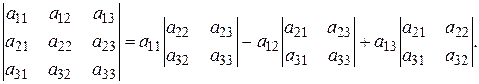 (2)
(2) называется определитель, полученный из исходной матрицы путем вычеркивания в ней i-й строки и j-го столбца. Обозначается этот минор как
называется определитель, полученный из исходной матрицы путем вычеркивания в ней i-й строки и j-го столбца. Обозначается этот минор как  . Алгебраическим дополнением к элементу
. Алгебраическим дополнением к элементу  называется число, вычисляемое по формуле:
называется число, вычисляемое по формуле: 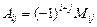 . С учетом этих обозначений формулу (2) можно переписать:
. С учетом этих обозначений формулу (2) можно переписать: . (3)
. (3)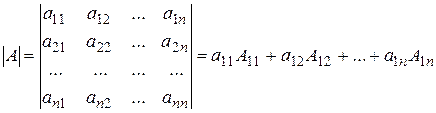 . (4)
. (4)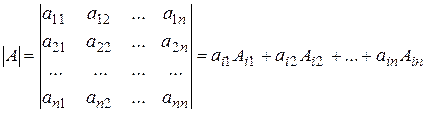 , (5)
, (5) , (6)
, (6) ; б)
; б) 
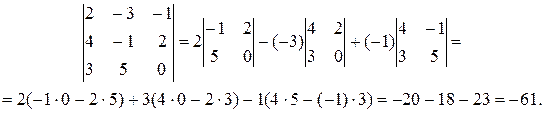
 .
.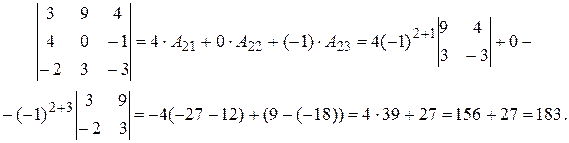

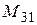 и алгебраическое дополнение
и алгебраическое дополнение 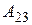 для матрицы
для матрицы 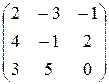 .
.
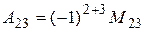 ,
, 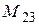 - это определитель матрицы, полученной из исходной путем вычеркивания 2-й строки и 3-го столбца. Поэтому
- это определитель матрицы, полученной из исходной путем вычеркивания 2-й строки и 3-го столбца. Поэтому
 ; б)
; б) 
 .
.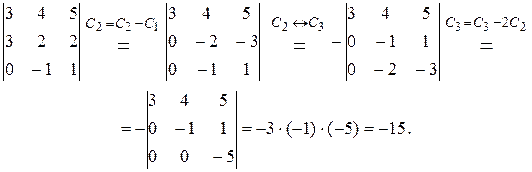
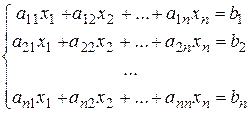 . (7)
. (7)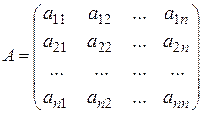 , составленная из коэффициентов системы (7), называется матрицей системы, а вектор
, составленная из коэффициентов системы (7), называется матрицей системы, а вектор  - столбцом (вектором) свободных членов.
- столбцом (вектором) свободных членов. ), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам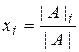 , i=1,2,…,n (8)
, i=1,2,…,n (8)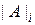 - определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
- определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.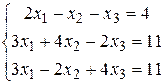 методом Крамера.
методом Крамера.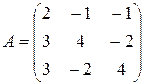 ,
,  . Далее вычисляем нужные определители:
. Далее вычисляем нужные определители: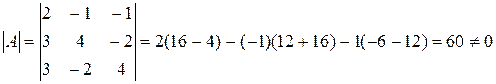 ;
;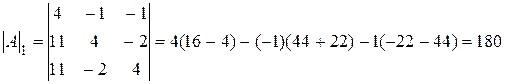
 ;
; .
. ;
;  ;
;  . Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы:
. Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы:  ,
,  ,
,  . Все уравнения обратились в тождества, следовательно, решение найдено верно.
. Все уравнения обратились в тождества, следовательно, решение найдено верно.


