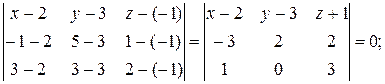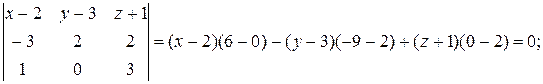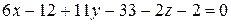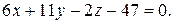ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
5.1. Предварительные сведения.Всюду далее предполагается, что на плоскости задана декартова (прямоугольная) система координат с осями OX, OY и началом координат в точке O(0;0). Расстояние от произвольной точки
расстояние между точками
Координаты точки C – середины отрезка [AB] – можно найти по формуле
Если соединить точки O(0;0) и 5.2. Прямая на плоскости. Среди различных уравнений прямой на плоскости наиболее распространенными можно считать следующие. Общее уравнение прямой на плоскости имеет вид
где A, B, C – вещественные числа (неравенство Уравнение прямой с угловым коэффициентом представляет собой уравнение, разрешенное относительно y:
Здесь k – угловой коэффициент прямой (тангенс угла, который прямая образует с положительным направление оси OX), а b – ордината точки пересечения прямой с осью OY. Следует заметить, что если k<0, то прямая образует с положительным направлением оси OX тупой угол; если k>0, то угол между прямой и осью OX острый. При k=0 прямая параллельна оси OX. Наконец, для прямой, перпендикулярной оси OX, угловой коэффициент не определен, а ее уравнение имеет вид x=const. Параметрическое уравнение прямой имеет вид
где
Наконец, при построении прямой очень удобным является уравнение прямой в отрезках записывается в виде
где a и b – соответствующие координаты точек пересечения прямой с осью OX (точка A(a;0)) и OY (точка B(0;b)). Например, прямая Пример 5.1. Дана прямая Решение. Сравнивая уравнение данной прямой с (14), замечаем, что в нашем случае Чтобы найти угловой коэффициент, исходное уравнение необходимо разрешить относительно y: Как известно, для построения прямой необходимо знать координаты двух точек, через которые проходит прямая. Одна из них, точка пересечения прямой и оси OY, известна; ее координаты (0;2/5). При Замечание. Для построения прямой можно было привести исходное уравнение к виду «в отрезках»: Пример 5.2. Прямая задана параметрическим уравнением Решение. В соответствии с уравнением (16) Вектор нормали связан с общим уравнением прямой, а чтобы перейти к нему, необходимо в одном из заданных уравнений выразить t через x, и полученное выражение подставить во второе уравнение. Например, из первого уравнения 5.3. Угол между прямыми. Чтобы найти угол между двумя прямыми, заданными уравнениями с угловым коэффициентом (
Из (19) вытекают условия параллельности ( Пример 5.3. Выбрать из прямых (I) – (V) параллельные и перпендикулярные, определить угол между прямыми (I) и (VI): (I) (IV) Решение. Сначала для каждой прямой найдем угловой коэффициент: (I): (II): (III) (IV) (V) (VI) Поскольку 5.4. Составление уравнений прямых. Рассмотрим основные типы возникающих задач. 1) Записать уравнение прямой с известным угловым коэффициентом Ответом является уравнение
Пример 5.4. Составить уравнение прямой, проходящей через точку A(2,-3) и образующей с положительным направлением оси OX угол 1200. Решение. Координаты точки известны, а угловой коэффициент 2) Записать уравнение прямой, проходящей через заданную точку
3) Записать уравнение прямой, проходящей через точку
Пример 5.5. Составить уравнения прямых, проходящих через точку A(2,-3) параллельно и перпендикулярно прямой Решение. Найдем угловой коэффициент данной прямой. Из исходного уравнения Результат можно проверить, подставив в полученное выражение координаты заданной точки: Аналогично действуем при составлении уравнения перпендикулярной прямой, только используем (22): 4) Записать уравнение прямой, проходящей через две заданные точки Подставив поочередно координаты точек в (15) и решив систему двух уравнений с двумя неизвестными, можно получить уравнение
Пример 5.6. Написать уравнение прямой, проходящей через точки A(3;4) и B(-1;5). Решение. Подставляя в (23) координаты данных точек, получаем:
Собирая теперь все в одну сторону, приходим к уравнению Замечание. В некоторых задачах нужно найти точку пересечения заданных прямых. Для этого решается система уравнений, определяющих эти прямые. Пример 5.7. В треугольнике с вершинами O(0;0), A(3;3), B(-1;5) найти уравнение стороны AB, медианы AE и высоты OK, а также длину высоты OK. Решение. У равнения стороны AB получим так же, как при решении примера 5.6:
Собирая теперь все в одну сторону, приходим к уравнению Далее, по определению медианы треугольника точка E – середина отрезка BO, поэтому ее координаты можно найти по формуле (13):
Таким образом, теперь надо составить уравнение прямой, проходящей через точки A(3;3) и E(-1/2;5/2). Подставляем их координаты в (23):
Итак, уравнение медианы AE имеет вид Далее, высота OK – это прямая, проходящая через вершину O перпендикулярно прямой AB. Воспользуемся уравнением (22). Угловой коэффициент Теперь найдем координаты K – точки пересечения построенной высоты и прямой AB. Решаем систему уравнений:
Итак, K(9/5; 18/5). В силу (11) 5.5. Полуплоскости и системы линейных неравенств. Неравенство Пример 5.8. Решить графически системы линейных неравенств: a) Решение. Сначала надо построить все прямые (рассмотрев соответствующие равенства); затем из каждого неравенства выразить y и определить требуемую полуплоскость; затем найти пересечение полученных полуплоскостей. В случае a) прямая
Случай b) отличается добавленным неравенством 5.6. Прямая и плоскость в пространстве. В пространстве уравнение
задает плоскость, а прямая определяется как пересечение двух плоскостей:
(плоскости не могут быть параллельны, т.е. коэффициенты A1, B1, C1 не могут быть пропорциональны коэффициентам A2, B2, C2).Ууравнения (25) называются общими уравнениями прямой в пространстве. Канонические уравнения прямой в пространстве имеют вид
а параметрические –
где, как и ранее, Пример 5.9. Написать параметрические, канонические и общие уравнения прямой, проходящей через точки A(-1;2;4) и B(2;5;3). Решение. В качестве точки, лежащей на плоскости, можно взять любую из заданных; пусть, для определенности, это будет точка A. Направляющим вектором прямой является вектор
Таким образом, Чтобы составить общие уравнения, необходимо из одного из параметрических уравнений выразить t и подставить полученное выражение в оставшиеся уравнения. Например, в данном примере из третьего уравнения получаем t=4-z, и поэтому Канонические уравнения выписываем по формуле (26):
Замечание 1. При составлениипараметрического уравнения можно было в качестве направляющего вектора взять Замечание 2. При составлении канонических уравнений прямой, проходящей через точки A(xA;yA;zA) и B(xB;yB;zB), можно использовать правило
(проверьте, что при применении (28) в примере 5.9 получается тот же самый результат, что и при использовании (26)). Ряд задач аналитической геометрии решается с помощью систем линейных алгебраических уравнений, вычислений определителей и т.д. Пример 5.10. Составить уравнение плоскости, проходящей через точки A(2;3;-1), B(-1; 5;1), C(3; 3; 2). Решение. Как известно, через три точки, не лежащие на одной прямой, можно провести единственную плоскость. Ее уравнение имеет вид:
Подставим в эту формулу координаты наших точек и раскроем определитель по первой строке:
и окончательно: Замечание. Для проверки достаточно последовательно подставить в полученное уравнение координаты всех точек и убедиться, что каждый раз уравнение превращается в тождество. Например, для точки A(2;3;-1): 12+33+4-47º0.
|

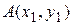 до начала координат задается формулой
до начала координат задается формулой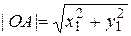 (11)
(11)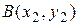 - формулой
- формулой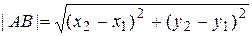 . (12)
. (12)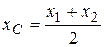 ;
; 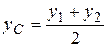 (13).
(13).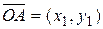 , длина которого задается формулой (11). Если аналогичным образом соединить
, длина которого задается формулой (11). Если аналогичным образом соединить 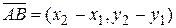 , длина которого находится по формуле (12).
, длина которого находится по формуле (12).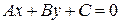 ,
,  (14)
(14)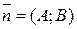 называется вектором нормали и перпендикулярен данной прямой.
называется вектором нормали и перпендикулярен данной прямой.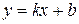 (15)
(15)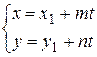 ,
, 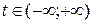 (16)
(16)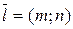 - направляющий вектор прямой. Из (16) можно получить каноническое уравнение прямой:
- направляющий вектор прямой. Из (16) можно получить каноническое уравнение прямой: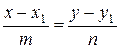 . (17)
. (17)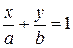 , (18)
, (18)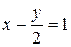 проходит через точки A(1;0) и B(0;-2), а прямая
проходит через точки A(1;0) и B(0;-2), а прямая 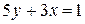 через точки A(1/3;0) и B(0;1/5); (так как уравнение
через точки A(1/3;0) и B(0;1/5); (так как уравнение 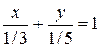 .
.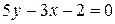 . Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.
. Выписать ее вектор нормали, найти угловой коэффициент, построить прямую на плоскости.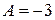 (коэффициент при x),
(коэффициент при x), 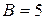 (коэффициент при y), поэтому
(коэффициент при y), поэтому 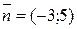 .
.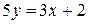 ;
;  . Сравнивая с уравнением (15), замечаем, что k=3/5.
. Сравнивая с уравнением (15), замечаем, что k=3/5.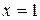 из последнего уравнения получаем, что
из последнего уравнения получаем, что 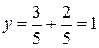 . Итак, остается провести прямую, проходящую через точки A(0; 2/5), B(1; 1).
. Итак, остается провести прямую, проходящую через точки A(0; 2/5), B(1; 1).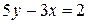 ;
; 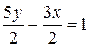 ;
; 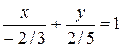 . Теперь достаточно отложить на оси OX значение «-2/3», а на оси OY значение 2/5, и провести через полученные точки прямую.
. Теперь достаточно отложить на оси OX значение «-2/3», а на оси OY значение 2/5, и провести через полученные точки прямую.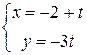 ,
, 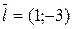 , а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1
, а точка A(-2;0) лежит на прямой. Чтобы найти координаты второй точки, лежащей на прямой, зададим какое-нибудь значение параметра t. В частности, при t=1 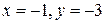 , т.е. точка B(-1;-3) принадлежит прямой.
, т.е. точка B(-1;-3) принадлежит прямой.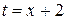 , следовательно,
, следовательно, 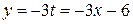 . Окончательно имеем:
. Окончательно имеем: 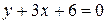 ,
, 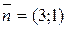
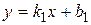 ,
, 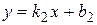 ), необходимо воспользоваться формулой
), необходимо воспользоваться формулой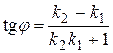 . (19)
. (19)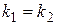 ) и перпендикулярности двух прямых (
) и перпендикулярности двух прямых (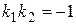 ).
). ; (II)
; (II) 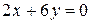 ; (III)
; (III) 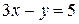 ;
;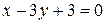 ; (V)
; (V) 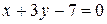 ; (VI)
; (VI) 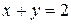 .
.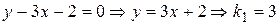 ;
;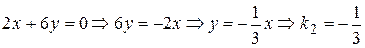 ;
;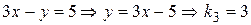 ;
;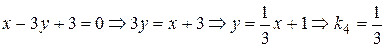 ;
;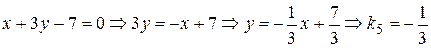 ;
;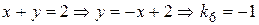 .
.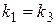 ,
, 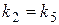 , получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны,
, получаем, что прямые (I) и (III), (II) и (V) параллельны. С другой стороны, 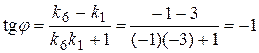 . Но тогда
. Но тогда 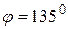 .
.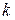 , проходящей через заданную точку
, проходящей через заданную точку 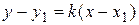 . (20)
. (20)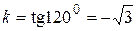 . Подставляя данные в (20), получаем:
. Подставляя данные в (20), получаем: 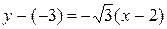 или, собрав все в одну сторону равенства,
или, собрав все в одну сторону равенства, 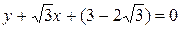 .
.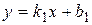 . Для решения используем уравнение (20) и учтем, что угловые коэффициенты параллельных прямых совпадают:
. Для решения используем уравнение (20) и учтем, что угловые коэффициенты параллельных прямых совпадают: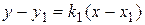 . (21)
. (21)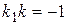 , поэтому
, поэтому  . Остается подставить это в (20) и получить уравнение:
. Остается подставить это в (20) и получить уравнение: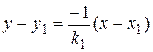 . (22)
. (22)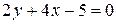 .
. получаем, что
получаем, что 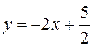 . Поэтому
. Поэтому 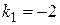 . Для прямой, проходящей через A(2,-3) параллельно данной прямой, воспользуемся уравнением (21):
. Для прямой, проходящей через A(2,-3) параллельно данной прямой, воспользуемся уравнением (21): 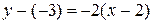 или
или 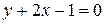 .
.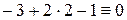 (если получили тождество, как в данном примере, уравнение составлено правильно).
(если получили тождество, как в данном примере, уравнение составлено правильно).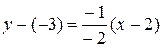 ,
, 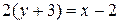 , и окончательно
, и окончательно 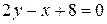 .
.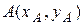 ,
, 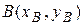 .
.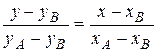 . (23)
. (23)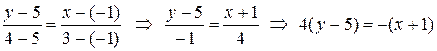 .
.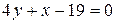 . Проверить результат можно, подставляя в него координаты точек (как при проверке в примере 5.5). Действительно,
. Проверить результат можно, подставляя в него координаты точек (как при проверке в примере 5.5). Действительно, 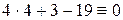 ,
, 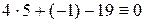 .
.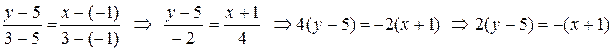 .
.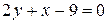 .
.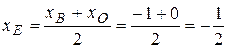 ,
, 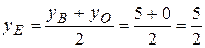 .
.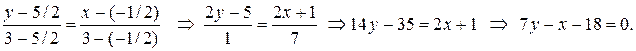
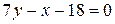 .
.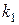 прямой AB находим из уравнения
прямой AB находим из уравнения 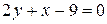 :
: 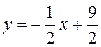 , поэтому
, поэтому 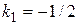 . Тогда имеем:
. Тогда имеем: 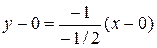 , и уравнение высоты OK
, и уравнение высоты OK 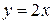 .
.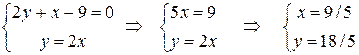 .
.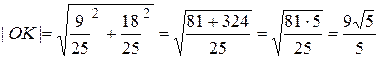 .
.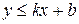 определяет полуплоскость, лежащую ниже прямой
определяет полуплоскость, лежащую ниже прямой 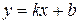 , неравенство
, неравенство 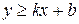 - полуплоскость, лежащую выше этой прямой. В обоих случаях прямая включается в полуплоскость и на рисунке изображается сплошной линией. Для строгих неравенств прямая в полуплоскость не включается и изображается пунктиром. Решить систему линейных неравенств – значит найти пересечение полуплоскостей, задаваемых каждым из неравенств, а затем определить координаты найти вершин полученной области.
- полуплоскость, лежащую выше этой прямой. В обоих случаях прямая включается в полуплоскость и на рисунке изображается сплошной линией. Для строгих неравенств прямая в полуплоскость не включается и изображается пунктиром. Решить систему линейных неравенств – значит найти пересечение полуплоскостей, задаваемых каждым из неравенств, а затем определить координаты найти вершин полученной области.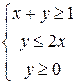 b)
b) 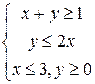 .
.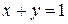 проходит через точки (0;1) и (1;0), а фигурирующее в системе неравенство определяет полуплоскость, лежащую выше этой прямой (так как
проходит через точки (0;1) и (1;0), а фигурирующее в системе неравенство определяет полуплоскость, лежащую выше этой прямой (так как 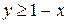 ). Прямая
). Прямая 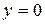 и имеет координаты A(1,0); вершина B образована пересечением прямых
и имеет координаты A(1,0); вершина B образована пересечением прямых 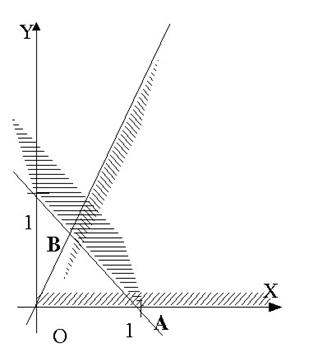
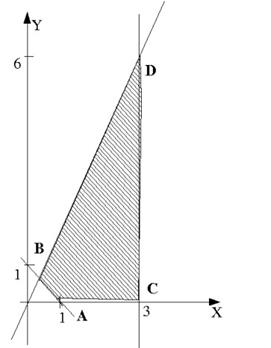
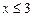 . Результат построений изображен на рисунке 5.2 (с.41). В данном случае пересечение всех полуплоскостей – замкнутая область, четырехугольник ABDC. Остается найти координаты вершин. A(1;0) и B(1/3;2/3) уже известны. Точка C – пересечение прямых
. Результат построений изображен на рисунке 5.2 (с.41). В данном случае пересечение всех полуплоскостей – замкнутая область, четырехугольник ABDC. Остается найти координаты вершин. A(1;0) и B(1/3;2/3) уже известны. Точка C – пересечение прямых 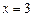 ,
, 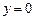 , т.е. C(3;0). Аналогично D имеет координаты D(3;6) как точка пересечения прямых
, т.е. C(3;0). Аналогично D имеет координаты D(3;6) как точка пересечения прямых 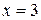 ,
,  (
(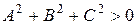 ) (24)
) (24)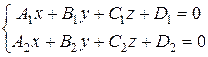 (25)
(25) , (26)
, (26)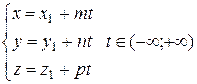 , (27)
, (27)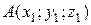 – точка, лежащая на прямой, а
– точка, лежащая на прямой, а 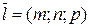 - направляющий вектор прямой.
- направляющий вектор прямой.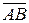 , координаты которого находятся по правилу, сформулированному в конце п.5.1:
, координаты которого находятся по правилу, сформулированному в конце п.5.1: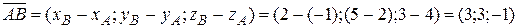 .
.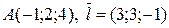 и в силу (27) параметрические уравнения имеют вид
и в силу (27) параметрические уравнения имеют вид 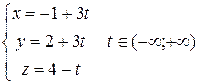 .
.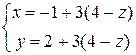 или окончательно
или окончательно 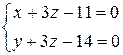 .
.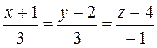 .
.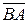 , а в качестве лежащей на прямой точки – B.
, а в качестве лежащей на прямой точки – B.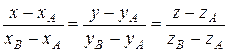 (28)
(28)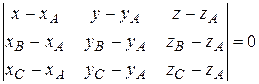 .
.