И твердых тел. Броуновское движение
Число степеней свободы - это число независимых переменных, которыми определяется состояние системы. Для того чтобы полностью охарактеризовать состояние материальной точки в некоторый момент времени, необходимо задать три координаты. Для описания состояния многоатомной молекулы, содержащей N атомов, необходимо задать 3N чисел, т.е.
Это полное число механических степеней свободы многоатомной системы. В молекулярной физике используют понятие статистических степеней свободы. Их число для многоатомной молекулы больше, чем число механических степеней свободы и может быть выражено через последнее. Число статистических степеней свободы равно числу квадратичных форм типа
На каждую степень свободы статистической системы приходится одна и та же средняя энергия, равная
При сообщении системе в некотором процессе a теплоты
Молярная теплоемкость при постоянном объеме определена как учитывая, что
принимает вид
Для идеальных твердых тел
В случае моноатомных твердых тел, т.е. состоящих из одного сорта атомов, например, металлов
что соответствует закону Дюлонга-Пти. Для многокомпонент-ных кристаллов Достаточно мелкие частицы вещества, являющиеся, тем не менее, макроскопическими, т.е. состоящими из большого числа молекул, взвешенные в жидкости или газе, находятся в хаотическом непрерывном движении или дрожании. Такое движение называют броуновским. Поскольку энергия броуновской частицы много меньше энергии молекул окружающей среды, и вся система находится в термодинамическом равновесии, то на каждую степень свободы броуновской частицы приходится одна и та же средняя величина энергии, равная
|

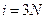 . (8.1)
. (8.1)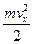 , с помощью которых записывают энергию многоатомной молекулы. Различают поступательные (
, с помощью которых записывают энергию многоатомной молекулы. Различают поступательные (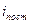 ), вращательные (
), вращательные (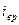 ) и колебательные (
) и колебательные (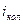 ) степени свободы. Максимальное число статистических степеней свободы многоатомной молекулы определяют следующим образом:
) степени свободы. Максимальное число статистических степеней свободы многоатомной молекулы определяют следующим образом: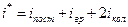 ,
, 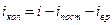 , (8.2)
, (8.2)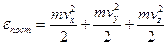 :
: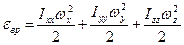 . Энергия одномерного колебания включает в себя кинетическую и потенциальную составляющие:
. Энергия одномерного колебания включает в себя кинетическую и потенциальную составляющие: 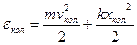 .
.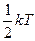 . Средняя энергия многоатомной молекулы в целом равна
. Средняя энергия многоатомной молекулы в целом равна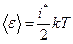 . (8.3)
. (8.3)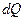 ee температура изменяется на
ee температура изменяется на 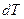 . Величина, равная
. Величина, равная 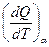 , называется теплоемкостью. Теплоемкость единицы массы вещества называется удельной (
, называется теплоемкостью. Теплоемкость единицы массы вещества называется удельной (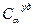 ), а одного моля – молярной (
), а одного моля – молярной (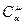 ). Молярные теплоемкости идеального газа при постоянном объеме и давлении
). Молярные теплоемкости идеального газа при постоянном объеме и давлении 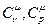 связаны соотношением
связаны соотношением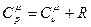 . (8.4)
. (8.4)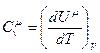 , (8.5)
, (8.5)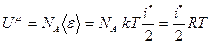 , выражение
, выражение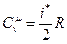 . (8.6)
. (8.6)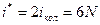 , согласно (8.2), так как
, согласно (8.2), так как  ,
, 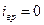 . Кроме того,
. Кроме того,
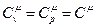 . (8.7)
. (8.7)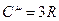 , (8.8)
, (8.8) различны и определяются формулой (8.6).
различны и определяются формулой (8.6).


