З а д а ч и. 9.1. На основе обобщённого уравнения переноса получить зависимость коэффициентов переноса (D,k,h) от микроскопических и макроскопических параметров системы.

9.1. На основе обобщённого уравнения переноса получить зависимость коэффициентов переноса (D,k,h) от микроскопических и макроскопических параметров системы.

9.2. Для измерения теплопроводности азота им наполнили пространство между двумя длинными коаксиальными цилиндрами, радиусы которых r₁ = 0,5 см и r₂ = 2 см. Внутренний цилиндр равномерно нагревается спиралью, по которой проходит ток силой i = 0,1 А. Сопротивление спирали, приходящееся на единицу длины цилиндра, равно R = 0,1 Ом. Внешний цилиндр поддерживается при температуре t₂ = 0°C. При установившемся процессе оказалось, что температура первого цилиндра t₁ = 93°C. Найти газокинетический диаметр молекулы азота. Давление газа таково, что конвекцией можно пренебречь.

9.3. Пользуясь полученной в задаче 9.1. зависимостью k(T), найти стационарное распределение температуры в плоско-параллельном слое газа толщины l, на границах которого поддерживаются постоянные температуры T₁ и T₂. Нагревание производят таким образом, что конвекции не возникает. Найти также стационарное распределение температуры для сферичес-

кого и цилиндрического слоёв.

 

9.4. Через тонкую трубку (l >> 2r) течёт ультраразреженный газ. Оценить число молекул N, ежесекундно проходящих через поперечное сечение трубки длины l, если на одном её конце концентрация молекул n₁, а на другом – n₂. Течение считать изотермическим.

 

9.5. Определить, на какой угол j повернётся диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см. вращается второй такой же диск с угловой скоростью w = 50 рад/с. Радиус дисков R = 10 см, модуль кручения нити f = 100 дин×с/см. Краевыми эффектами пренебречь. Движение воздуха между дисками считать ламинарным.

 

9.6. Решить предыдущую задачу в предположении, что диски помещены в сильно разреженный воздух с P = 10^-4мм.рт.ст., когда l молекул воздуха велика по сравнению с расстоянием между дисками. Для упрощения расчёта считать, что все молекулы движутся с одинаковыми по абсолютному значению скоростями, равными средней скорости молекул воздуха V = 450 м/с.

 

9.7. Определить расход массы газа Q при стационарном изотермическом пуазейлевом течении его вдоль цилиндрической трубы длины l и радиуса r, на концах которой поддерживается давление P₁ и P₂ (P₁ > P₂).

 

9.8. Для определения вязкости h углекислого газа им наполнили колбу с объёмом V = 1 л при давлении P₁ = 1600 мм.рт.ст. Затем открыли кран, позволяющий CO₂ вытекать из сосуда через капилляр длиною l = 10 см и диаметром D = 0,1 мм. Через время t = 22 мин давление в колбе понизилось до P₃ = 1350 мм.рт.ст. Вычислить из этих данных h и газокинетический

 

диаметр молекулы CO₂. Атмосферное давление P₂ = 735 мм. рт. ст. Процесс считать изотермическим при температуре 15°C.

 

О т в е т ы

9.1. , .

 

9.2. .

9.3.

для плоскопараллельного слоя =

для сферического слоя ,

для цилиндрического слоя .

9.4. .

9.5. .

9.6. .

9.7. .

 

 

9.8. ,

.
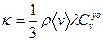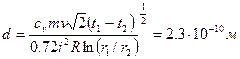
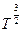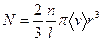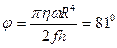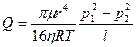