З а д а ч и.
5.2. Исходя из распределения Максвелла, найти следующие величины:
5.3. Получить выражение для среднего квадрата x-компоненты скорости молекулы газа. Найти среднюю кинетическую энергию, приходящуюся на одну степень свободы поступательного движения молекулы газа.
5.4. Используя распределение Максвелла по одной компоненте скорости, получить выражение для давления на стенку сосуда. 5.5. Найти отношение числа молекул водорода
5.6. Получить выражения для трех характерных скоростей распределения Максвелла.
5.7. Найти среднее значение обратной величины скорости молекулы в газе.
5.8. Написать выражение для среднего числа 5.9. Найти наивероятнейшее значение кинетической энергии
5.10. Показать, что если за единицу скорости молекул газа принять наиболее вероятную скорость, то число молекул, абсолютные значения скоростей которых лежат между V и V + dV, не будет зависеть от температуры газа.
5.11. Найти среднее число молекул, компоненты скорости которых, параллельные некоторой оси, лежат в интервале
5.13. Найти полную кинетическую энергию Е молекул одноатомного газа, ударяющихся о квадратный сантиметр стенки в единицу времени. Задачу решить сначала в общем виде для изотропной функции распределения, а затем применить результат к частному случаю максвелловского распределения. О т в е т ы 5.1.
5.2. Значения всех величин равны нулю. 5.3. 5.4. 5.5. a) 5.6. 5.7. 5.8. 5.9. 5.10. 5.11.
5.12. 5.13. Для изотропного распределения Для распределения Максвелла
|

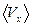 ,
, 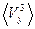 ,
, 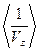 .
. , если температура водорода 300°С: а) число частиц
, если температура водорода 300°С: а) число частиц  имеют скорости от 3000 м/c до 3010 м/с, а
имеют скорости от 3000 м/c до 3010 м/с, а  - в пределах от 1500 м/c до 1510 м/c; б) для
- в пределах от 1500 м/c до 1510 м/c; б) для  молекул газа, кинетические энергии которых заключены между
молекул газа, кинетические энергии которых заключены между  и
и  .
. , при котором в фиксированный интервал энергии
, при котором в фиксированный интервал энергии 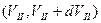 , а абсолютные значения перпендикулярной составляющей скорости заключены между
, а абсолютные значения перпендикулярной составляющей скорости заключены между  и
и 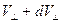 .
.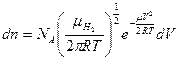 , подставив данные
, подставив данные (постоянная Авогадро),
(постоянная Авогадро),  , T =300K, V =500 м/с,
, T =300K, V =500 м/с,  =2 м/с, R =8,31
=2 м/с, R =8,31 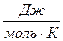 , получаем
, получаем 
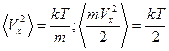 .
. концентрация идеального газа.
концентрация идеального газа. , б)
, б) 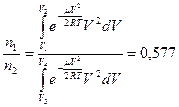 .
.
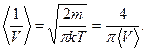
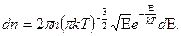
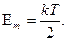

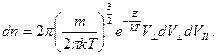

 .
. .
.


