Семинар 4. Распределение Гиббса
Одной из важных проблем молекулярной физики является распределение энергии eо между различными частями изолированной системы. Совокупность незамкнутых систем, имеющих возможность обмениваться энергией только между собой, называется каноническим ансамблем. На вопрос, какова вероятность того, что система имеет некоторую энергию
где А – нормировочная константа, ga – число микросостояний системы с энергией
где
где dg=p (
называется плотностью состояний системы в интервале [ Статистической суммой называется величина Z:
В случае непрерывного распределения энергии:
здесь интегрирование ведется по всей области определения энергии системы. Учитывая условие нормировки, получаем
С помощью статистической суммы Z можно формализовать вычисление среднего значения энергии и ее дисперсии:
|

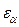 , при условии что ea<<eо, отвечает распределение Гиббса, или каноническое распределение:
, при условии что ea<<eо, отвечает распределение Гиббса, или каноническое распределение: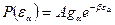 (4.1)
(4.1)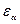 (кратность вырождения),
(кратность вырождения), 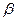 - параметр, определяющий термодинамическую температуру:
- параметр, определяющий термодинамическую температуру: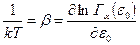 , (4.2)
, (4.2)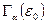 – число доступных состояний канонического ансамбля, посредством которых осуществляется состояние с нулевой энергией у рассматриваемой системы. Формула (4.2) дает первичное статистическое определение температуры. В случае непрерывного распределения энергии вероятность того, что система находится в состоянии с энергией в интервале между
– число доступных состояний канонического ансамбля, посредством которых осуществляется состояние с нулевой энергией у рассматриваемой системы. Формула (4.2) дает первичное статистическое определение температуры. В случае непрерывного распределения энергии вероятность того, что система находится в состоянии с энергией в интервале между 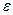 и
и 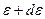 равна
равна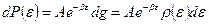 (4.3)
(4.3)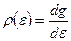 (4.4)
(4.4)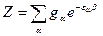 (4.5)
(4.5)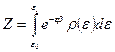 (4.6)
(4.6)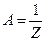 (4.7)
(4.7)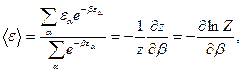 (4.8)
(4.8)