З а д а ч и. 1.1. В сосуде находятся 5 молекул газа
1.1. В сосуде находятся 5 молекул газа. Мысленно разобьем сосуд на две равные части. Каждая из молекул может находиться в выделенной половине объема или не находиться в ней. Рассмотреть "макроскопическое" состояние, когда m молекул газа находятся в выделенной половине сосуда, и найти число микроскопических состояний Гm, с помощью которых оно реализуется. Принять m равным 0, 1, 2, 3, 4, 5. Определить также общее число микросостояний Г0 и частоту реализации всех рассмотренных «макросостояний». Термин «макроскопическое состояние» здесь использован условно, поскольку в системе всего 5 частиц, и она, строго говоря, не является статистической. По этой же причине вместо «вероятность» употребляется термин «частота».
1.2. В системе из n частиц со спином 1/2 в отсутствии внешнего магнитного поля спин каждой частицы может быть равновероятно ориентирован либо вверх, либо вниз. а) Найти вероятность Pn(m) реализации состояния, когда m спинов направлены вверх. б) Построить гистограмму зависимости P(m) для n =6. Как будет изменяться вид распределения P(m) при увеличении чисел n и m? Чему равно наивероятнейшее значение m?
1.3. Состояние системы характеризуется случайной величиной x с известным распределением вероятности: а) в) Найти нормировочную константу А для каждого случая. Построить соответствующие графики плотности вероятности.
1.4. Проверить выполнение условия нормировки вероятности в задаче 1.1.
1.5. Представим себе тонкую медную проволоку, натянутую вдоль оси Х. Несколько атомов меди, расположенных вблизи х =0, сделали "мечеными" (радиоактивными). При увеличении температуры нити подвижность атомов возрастает. При этом каждый атом может перескочить на соседнее место в кристаллической решетке либо направо, либо налево. Параметр решетки равен l. Предположим, что в момент времени t =0 температура нити быстро возрастает до некоторого большого значения и в дальнейшем остается неизменной, т.е. до момента t =0 атомы "не прыгали", а покоились в узлах решетки, в том числе и "меченые" атомы в окрестности x =0. Вероятность того, что радиоактивный атом будет обнаружен по истечении времени t при условии, что t>>t (t - время нахождения атома в узлах решетки), в интервале [x, x+dx] определяется плотностью вероятности f(x), dP(x) = f(x)dx. Изобразить на графике примерный ход плотности вероятности в зависимости от x, исходя из соображений симметрии и условия нормировки, для следующих трех случаев: а) вскоре после t =0, б) по прошествии относительно большого времени t, в) по прошествии очень большого времени t.
О т в е т ы 1.1. Гm =1; 5; 10; 10; 5; 1. Г0 = 32. 1.2. а) Pn(m) = б) С ростом числа частиц в системе n гистограмма переходит в график непрерывного распределения вероятности. Кривая представляет собой очень высокий и узкий пик, максимум которого находится при mн = n /2.
1.3. а) 1.5. Площади под кривыми f(x) во всех случаях одинаковы и равны единице. Это условие нормировки плотности вероятности.
|

 б)
б) 
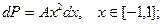 г)
г) 
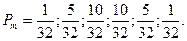
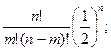
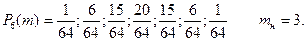
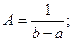 б) А=2; в)
б) А=2; в) 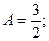 г)
г)