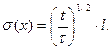З а д а ч и. 2.1. Получить формулу (2.3) для вычисления дисперсии.
2.1. Получить формулу (2.3) для вычисления дисперсии.
первом случае проекция магнитного момента на направление поля равна m0, во втором – m0. Определить ámñ;, ám2ñ;, s2(m).
2.4. Рассмотрим ядро со спином 1. Проекция магнитного момента этого ядра вдоль направления магнитного поля может иметь три возможных значения, а именно +m0, 0 и -m0. Пусть вероятность того, что m = + m0 будет р, и вероятность того, что m = - m0, также р. а) Из условия нормировки определить вероятность того, что m = 0. б) Вычислить ámñ, ám2ñ, s2(m).
2.5. Пусть F – какая-либо аддитивная физическая величина, характеризующая систему N молекул идеального газа, так что Примечание: Величины f и g называют статистически независимыми, если
2.6. Предположим, что твердое тело содержит N ядер, удовлетворяющих условию задачи 2.3, и их взаимодействием с другими ядрами можно пренебречь. Обозначим через М полную проекцию магнитного момента вдоль заданного направления. Выразить áМñ; и его стандартное отклонение через N, р и m0, используя результаты задачи 2.5. В случае затруднения адресуем к [4].
2.7. Используя условие задачи 1.5, а) определить, на какое среднее расстояние áхñ; от начала координат смещается радиоактивный атом за время t; б) получить формулу для стандартного отклонения смещения s(х) радиоактивного атома за время t.
Ответы 2.2.
2.3.
2.4.
2.5.
2.6.
2.7. а)
|


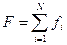 , где fi значение f для i -ой частицы газа. Выразить абсолютную и относительную меры флуктуаций (s и a) величины F через средний квадрат флуктуации величины f.
, где fi значение f для i -ой частицы газа. Выразить абсолютную и относительную меры флуктуаций (s и a) величины F через средний квадрат флуктуации величины f. . Для них справедливо равенство
. Для них справедливо равенство 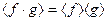 .
.
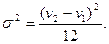
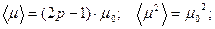
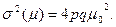
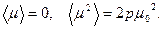
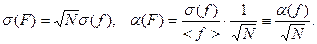
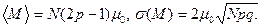
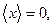 б)
б)