Семинары 5, 6. Распределение Максвелла
В состоянии теплового равновесия частицы идеального газа имеют различные скорости, которые меняются и результате столкновений. На вопрос какова вероятность того, что частица обладает определенной скоростью, отвечает распределение Максвелла. Оно является частным случаем распределения Гиббса, когда энергия частицы есть только ее кинетическая энергия:
где
При решении некоторых задач удобно пользоваться распределением Максвелла по отдельным компонентам скоростей:
– это вероятность того, что значение компоненты скорости В сферической системе координат распределение Максвелла, в случае изотропного пространства, имеет следующий вид:
Оно отвечает на вопрос какова вероятность того, что абсолютная скорость частицы лежит в интервале от
Следует отметить, что
На рис.5.2 приведен примерный вид плотностей вероятности распределения Максвелла для различных температур. Здесь же
показаны наивероятнейшие скорости каждого распределения. Как видно, они растут с увеличением температуры. Их значения можно получить, решая задачу на экстремум функции плотности вероятности:
Приведенные формулы распределения Максвелла позволяют находить средние значения различных микроскопических параметров, зависящих от скорости или ее отдельных компонент, в соответствии с общей процедурой усреднения. Если параметр зависит от абсолютной скорости -
Среднее значение параметра, зависящего от одной компоненты скорости, вычисляется по формуле
В случае, когда параметр зависит от двух или трех компонент скорости, для его усреднения следует использовать распределение (5.1). Характерными скоростями распределения Максвелла принято называть три величины: 1. Наивероятнейшая скорость - 2. Средняя скорость - 3. Средняя квадратичная скорость -
|

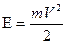 . В декартовой системе координат, в пространстве скоростей
. В декартовой системе координат, в пространстве скоростей 
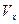 ,
, 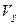 ,
, 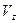 , распределение Максвелла имеет следующий вид:
, распределение Максвелла имеет следующий вид: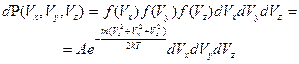 , (5.1)
, (5.1)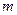 - масса частицы идеального газа. Постоянная
- масса частицы идеального газа. Постоянная 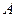 находится из условия нормировки:
находится из условия нормировки: (5.2)
(5.2) (5.3)
(5.3)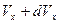 . Аналогичные выражения справедливы для вероятностей
. Аналогичные выражения справедливы для вероятностей 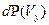 и
и 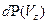 . Примерный вид плотности вероятности
. Примерный вид плотности вероятности  приведен на рис.5.1.
приведен на рис.5.1.
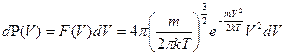 . (5.4)
. (5.4)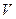 до
до 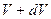 , а также на вопрос, сколько частиц
, а также на вопрос, сколько частиц  из
из 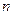 имеют абсолютную скорость в заданном интервале:
имеют абсолютную скорость в заданном интервале: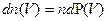 . (5.5)
. (5.5)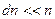 . Соответственно, доля частиц, имеющих абсолютную скорость в интервале от
. Соответственно, доля частиц, имеющих абсолютную скорость в интервале от 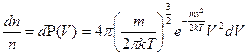 . (5.6)
. (5.6)
 . (5.7)
. (5.7) , то его среднее значение найдется вычислением интеграла
, то его среднее значение найдется вычислением интеграла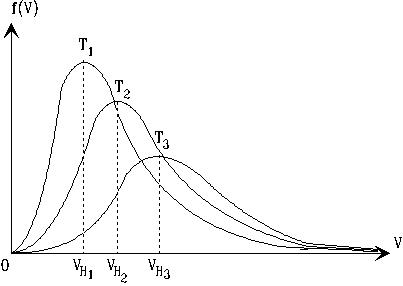
 . (5.9)
. (5.9) .
.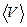 .
.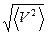 .
.


