З а д а ч и
7.1. Для определения числа Авогадро Перрен измерял распределение по высоте шарообразных частиц гуммигута, взвешенных в воде. Он нашел, что отношение
7.2. Методом статистической суммы найти среднюю потенциальную энергию молекулы воздуха в идеальной атмосфере (g=const, T=const на любой высоте). Вычислить молярную теплоемкость газа Сm. Считать, что молекулам газа доступна высота от нуля до бесконечности.
7.3. В теплоизолированный цилиндрический сосуд высоты H помещен моль идеального газа с относительной молекулярной массой
7.4. Для определения относительных молекулярных масс коллоидальных частиц исследуют распределение их концентрации в поле центробежной силы, возникающей при вращении центрифуги. Найти относительную молекулярную массу
7.5. Найти зависимость концентрации газа n0 (0)на оси вращения центрифуги от ее угловой скорости
7.6. Цилиндр радиуса R и длины H, наполненный химически однородным газом, равномерно вращается в однородном поле тяжести вокруг своей геометрической оси с угловой скоростью
О т в е т ы 7.1. 7.2. 7.3.
7.4. 7.6. Число молекул dN с координатами между r и r+dr, z и z+dz равно
где N - общее число молекул в сосуде.
|

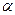 числа частиц в слоях, отстоящих друг от друга на расстояние l=30 мкм, равно 2,08. Плотности частиц
числа частиц в слоях, отстоящих друг от друга на расстояние l=30 мкм, равно 2,08. Плотности частиц 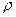 = 1,194 г/
= 1,194 г/ 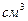 , воды
, воды 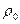 =1 г/
=1 г/ 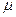 . Цилиндр подвешен в вертикальном положении в однородном поле тяжести. Температура газа в сосуде везде одинакова и равна T. Найти среднюю потенциальную энергию молекулы газа
. Цилиндр подвешен в вертикальном положении в однородном поле тяжести. Температура газа в сосуде везде одинакова и равна T. Найти среднюю потенциальную энергию молекулы газа 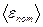 , теплоемкость этого газа, учитывая влияние поля тяжести и предполагая, что
, теплоемкость этого газа, учитывая влияние поля тяжести и предполагая, что 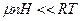 .
.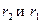 , равно
, равно 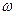 .
.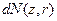 внутри цилиндра, если его ось направлена вертикально.
внутри цилиндра, если его ось направлена вертикально. .
.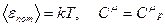 ,
,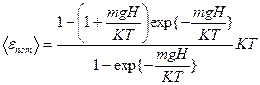 ,
,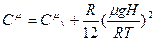 .
.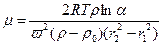 .
.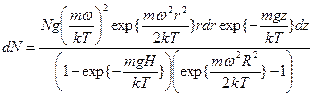 ,
,


