Физической статистики: вероятность, плотность вероятности, условие нормировки вероятности
Большинство событий в системе многих частиц (молекулярной системе) являются случайными. Закономерности, связанные со случайными величинами, изучаются теорией вероятности и математической статистикой. В теории вероятности [1,4] основным определением является частотное определение вероятности Р случайного события А:
где Ni – количество случаев, в которых наблюдается интересующий результат, N – общее число всех возможных случаев. Вероятность достоверного события (Ni = N) равна единице. Вероятность невозможного события равна нулю. В статистической физике вероятностью макроскопического состояния a системы называется величина Рa [3,4]:
где Г0 – общее число микросостояний, доступных для системы, Гa - число микросостояний, приводящих к данному макросостоянию a. Гa называют термодинамической вероятностью макроскопического состояния. Величины Г0 и Гa в ряде задач могут быть вычислены с помощью методов комбинаторики. Подробный вывод основных формул элементарной комбинаторики приведен в [3].
Основные формулы элементарной комбинаторики Число способов размещения m различных предметов по n местам:
Число способов размещения n различных предметов по n местам (число перестановок): Г2=n! (1.4) Число способов размещения m неразличимых предметов по n местам:
Число способов, которыми можно выбрать m различных предметов из n различных предметов, называется числом сочетаний и определяется выражением
Непрерывное распределение вероятности. Плотность вероятности. Условие нормировки вероятности Если состояние физической системы характеризуется параметром j, случайно принимающим любые значения от j0 до j1, то определение вероятности (1.1) лишено смысла, поскольку множество значений параметра не является счетным. В этом случае вероятность определяется в дифференциальной форме:
Утверждается, что dP(j) пропорциональна величине достаточно малого интервала изменений переменной dj, а коэффициент пропорциональности f(j) не зависит от величины этого интервала и называется плотностью вероятности [1,5]:
Знание плотности вероятности позволяет найти вероятность для любой области, в которой определена плотность. Рис.1
На рис.1
представлен пример графического изображения плотности вероятности. Площадь заштрихованной полоски на рисунке равна вероятности dP(j) нахождения величины j в интервале [j; j+dj]. Площадь под всей кривой f(j) есть вероятность нахождения величины j в интервале [j0;j1], которая всегда постоянна, равна 1 или 100% и определяет условие нормировки плотности вероятности.
Часто условие нормировки записывают для интервала значений j [0, ∞) или (-∞, +∞), полагая, что за пределами конечного интервала [j0,,j1] плотность вероятности равна нулю. Условие нормировки вероятности дискретно изменяющейся переменной j, которая может принимать n различных значений ji с соответствующей вероятностью Pi, записывается так:
Выражения (1.9) и (1.10) являются следствием теоремы сложения вероятностей для несовместных событий [1,4].
Условие нормировки есть математическая запись утверждения, что если физическая система существует, то она находится в каком-либо из доступных ей состояний, характеризующихся параметром j. Это событие является достоверным и его вероятность равна единице.
|

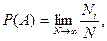 (1.1)
(1.1)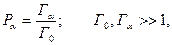 (1.2)
(1.2)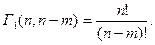 (1.3)
(1.3)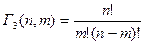 . (1.5)
. (1.5) (1.6)
(1.6)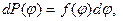 (1.7)
(1.7)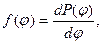 (1.8)
(1.8)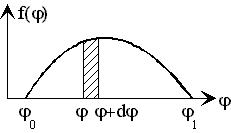
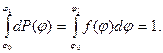 (1.9)
(1.9)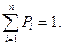 (1.10)
(1.10)


