Определение объема выборки
На стадии проектирования выборочного наблюдения рассчитывается объем выборки (n), который позволит получить величину ошибки, допустимую для конкретного исследования. Как отмечалось выше, величина ошибки выборки обратно пропорциональна ее объему. Однако увеличение объема выборки снижает эффективность затрат на проведение выборочного наблюдения, поэтому нужно искать компромисс между допустимой величиной ошибки и объемом выборки. Расчет объема выборки осуществляется, исходя из формулы ошибки выборки. Так:
(50)
Значение t зависит от устанавливаемого исследователем уровня вероятности и находится в таблице нормального распределения, поскольку в условиях больших выборок распределение ошибок подчиняется закону нормального распределения, или в таблице t-распределения Стьюдента, данному закону подчиняется распределение ошибок при малых выборках. Значение Правило трех сигм справедливо для нормального (симметричного) распределения. Если заведомо известно, что распределение единиц в изучаемой совокупности асимметрично (так, например, распределение населения по величине доходов всегда имеет правостороннюю асимметрию), значение дисперсии рассчитывают, исходя из того, что В рассматриваемой формуле расчета объема выборки ошибка выборки берется как абсолютная величина, но на практике она часто задается как относительная. Например, ошибка не должна превышать 2% или 5%. Тогда:
где
|
- величина ошибки выборки задается исследователем, исходя из целей и объекта исследования, обусловливающих необходимую точность получаемых оценок.
(дисперсии) берется по результатам предыдущих аналогичных исследований, если они проводились, и если за прошедшее время не произошло существенных изменений в изучаемой совокупности. Может быть проведено пилотное (пробное) исследование, и по его результатам рассчитана дисперсия. В противном случае используется «правило трех сигм» (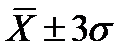
), исходя из которого в размах вариации (R = max - min) укладывается 6 
, следовательно: 
.
.
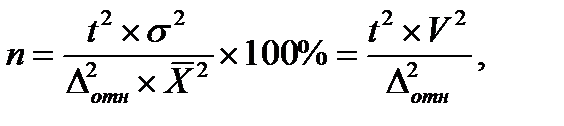(51)
, напомним, что V- это коэффициент вариации.
