Ошибки выборки
При проведении любого статистического наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При высоком уровне организации наблюдения их можно избежать. При проведении выборочных наблюдений возникают ошибки репрезентативности, которые связаны не с организацией наблюдения, а с самой сутью выборочного исследования, которая заключается в том, что по части (по выборочной совокупности) приходится судить о целом (о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что значения характеристик выборочной совокупности (показатели, рассчитанные по выборке), в той или иной степени, не совпадают со значениями аналогичных параметров генеральной совокупности. Задача исследователя состоит в том, чтобы сформировать репрезентативную выборку, позволяющую получить несмещенные оценки параметров генеральной совокупности и минимальную ошибку выборки. Основной принцип формирования выборки – случайность отбора, т.е. каждой единице в генеральной совокупности должна быть обеспечена равная вероятность попадания в выборку. Теоретической основой определения ошибки выборки являются теоремы Чебышева, Ляпунова и Бернулли. § Суть теоремы Чебышевасостоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией (вариацией), с вероятностью, близкой к единице, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины
n→∞, где На эти вопросы отвечает теорема Ляпунова,которая одновременно доказывает, что распределение ошибок выборки при больших объемах выборки подчинено нормальному закону распределения.Суть теоремы состоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией, вероятность того, что ошибка выборки не превысит величины tμ (предельная ошибка), равна нормированной функции Лапласа (Ф (t)):
где μ – средняя ошибка выборки, μ= Данная формула средней ошибки выборки не может быть использована на практике, так как при организации выборочного наблюдения формируется лишь одна выборка и исследователю не известна величина генеральной средней. Математической статистикой доказано, что величина μ2 прямо пропорциональна дисперсии генеральной совокупности (
Т.о., величина средней ошибки выборки прямо пропорциональна вариации признака в генеральной совокупности (хотя в практических расчетах вынужденно используется выборочная дисперсия ( В теореме Ляпунова речь идет о предельной ошибке, которую принято обозначать
Известно, что На практике нет необходимости рассчитывать величину t. Ее находят по таблице нормального распределения, исходя из установленного исследователем уровня вероятности. Социально-экономические исследования проводятся, как правило, с вероятностью Р=0,95. Согласно таблице нормального распределения, если Р=0,954, то t=1,96 Т.о., если исследователь устанавливает вероятность оценок 95%, то Представленная выше формула расчета ошибки выборки применима при проведении выборки методом повторного отбора. В статистике понятия «повторного» и «бесповторного» отбора соответствуют понятиям «возвратного» и «безвозвратного» шара в теории вероятности. При осуществлении повторного отбора, единицы совокупности, изъятые в выборку, возвращаются назад в генеральную совокупность и могут быть повторно выбраны в выборочную совокупность. При осуществлении бесповторной выборки единицы совокупности, изъятые в выборку, не возвращаются назад в генеральную совокупность и не могут быть повторно выбраны в выборочную совокупность. При повторном отборе от начала до конца вероятность попадания единиц в выборку сохраняется неизменной, т.е. При бесповторном отборе вероятность изменяется от Формула средней ошибки выборки для бесповторного отбора, который используется чаще, имеет вид:
Величина ошибки выборки зависит и от вида выборки. В формулах средней ошибки при реализации различных видов выборки используются разные дисперсии, для чего необходимо знание и понимание правило сложения дисперсий. Правило сложения дисперсий заключается в том, что общая дисперсия изучаемого признака есть сумма межгрупповой и внутригрупповой дисперсий. Пример: проведена группировка рабочих по признаку «наличие специального технического образования» и зафиксирован уровень производительности труда, результаты приведены в таблице 4.1. Таблица 4.1. Зависимость производительности труда рабочих (число деталей в смену) от наличия специального образования
Средний уровень производительности труда в целом по совокупности рабочих: Средний уровень производительности труда рабочих первой группы: Средний уровень производительности труда рабочих второй группы: Общая дисперсия:
Дисперсия каждой группы:
где
дисперсия второй группы:
На основе внутригрупповых дисперсий рассчитывается среднее значение внутригрупповой дисперсии:
Межгрупповая дисперсия:
(41)
Общая дисперсия – это дисперсия, характеризующая вариацию результативного признака под влиянием всех факторов. В данном случае она отражает степень варьирования уровня производительности труда рабочих под влиянием всех факторов, ее определяющих в конкретных условиях. Межгрупповая дисперсия характеризует вариацию признака (производительности труда), обусловленную вариацией группировочного признака (есть специальное техническое образование или нет). Внутригрупповая дисперсия оценивает вариацию признака, обусловленную всеми факторами, за исключением группировочного, поскольку внутри групп этот фактор не варьирует. В условиях собственно случайной выборки в формуле средней ошибки выборки используется общая дисперсия, поскольку в генеральной совокупности не выделяются группы (страты):
При стратифицированной выборке для расчета ошибки репрезентативности используется внутригрупповая дисперсия:
При серийной выборке в формуле средней ошибки выборки используется межгрупповая дисперсия, поскольку внутри отобранных серий проводится сплошное обследование, то вариация не носит характер случайной составляющей:
где r-число серий в выборочной совокупности; R- число серий в генеральной совокупности. Наибольшая величина ошибки возникает в условиях собственно случайной выборки. Стратифицированная и серийная выборки, позволяющие сформировать выборочную совокупность по структуре, закономерности распределения более близкую к генеральной совокупности, дают наименьшую величину ошибки (это демонстрируют и формулы расчета величины ошибки). Ошибка выборки для показателя доли единиц, обладающих тем или иным признаком. В практических исследованиях часто используется такая характеристика, как доля, доля единиц совокупности, обладающих тем или иным признаком, например: не абсолютное число рабочих, имеющих техническое образование, а их доля в общей численности; доля пенсионеров в общей численности населения города; доля инновационных предприятий в общем числе предприятий отрасли и т.п. Теоретической основой расчета ошибки выборки для доли служит теорема Бернулли, являющаяся частным случаем теоремы Чебышева (хотя исторически доказана раньше). При расчете средней ошибки доли используется формула, аналогичная формуле ошибки выборки для средней величины, но при этом учитывается дисперсия доли. Долю единиц, обладающих тем или иным значением признака (например, доля женщин среди работающего населения) в выборочной совокупности принято обозначать Средняя ошибка показателя доли рассчитывается:
где
|

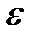 .
.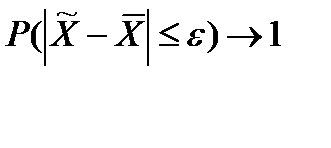 , (34)
, (34)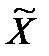 - выборочное среднее значение признака;
- выборочное среднее значение признака;  - генеральное среднее значение; Р - вероятность события, записанного в скобках. Суть события в том, что отклонение выборочной средней от генеральной сколь угодно мало, т.е. ошибка выборки при больших объемах выборки чрезвычайно мала и вероятность такого утверждения близка к 1. Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных. При этом остается неясным то, чему конкретно равна ошибка выборки, и с какой именно вероятностью можно гарантировать не превышение конкретной величины ошибки.
- генеральное среднее значение; Р - вероятность события, записанного в скобках. Суть события в том, что отклонение выборочной средней от генеральной сколь угодно мало, т.е. ошибка выборки при больших объемах выборки чрезвычайно мала и вероятность такого утверждения близка к 1. Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных. При этом остается неясным то, чему конкретно равна ошибка выборки, и с какой именно вероятностью можно гарантировать не превышение конкретной величины ошибки.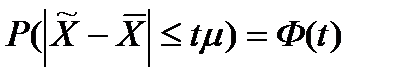 , (35)
, (35)
 ;
; 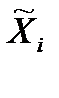 – среднее значение признака по i-й выборке; n- число выборок; tμ – предельная ошибка выборки
– среднее значение признака по i-й выборке; n- число выборок; tμ – предельная ошибка выборки ) и обратно пропорциональна объему выборки (n), т.е. μ2=
) и обратно пропорциональна объему выборки (n), т.е. μ2=  , следовательно, средняя ошибка выборки может быть рассчитана:
, следовательно, средняя ошибка выборки может быть рассчитана:  . В данной формуле предполагается использование дисперсии генеральной совокупности, величина которой исследователю не известна. Между выборочной (
. В данной формуле предполагается использование дисперсии генеральной совокупности, величина которой исследователю не известна. Между выборочной (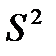 ) и генеральной(
) и генеральной( 2=S2
2=S2  . При большом объеме выборки
. При большом объеме выборки 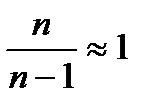 , поэтому на практике этот коэффициент игнорируют и в расчете средней ошибки используют величину выборочной дисперсии. Окончательная формула средней ошибки выборки:
, поэтому на практике этот коэффициент игнорируют и в расчете средней ошибки используют величину выборочной дисперсии. Окончательная формула средней ошибки выборки: . (36)
. (36) (
( ). Предельная ошибка – это t-кратное значение средней ошибки. Как же определяется величина t?
). Предельная ошибка – это t-кратное значение средней ошибки. Как же определяется величина t? - плотность нормального распределения, которому, согласно теореме, подчинено распределение ошибок больших выборок, где
- плотность нормального распределения, которому, согласно теореме, подчинено распределение ошибок больших выборок, где  . В условиях выборочного наблюдения
. В условиях выборочного наблюдения  - нормированное отклонение выборочной и генеральной средних.
- нормированное отклонение выборочной и генеральной средних.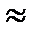 2; если Р=0,997, t
2; если Р=0,997, t  3.
3.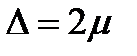 , то есть величина предельной ошибки равна двукратному значению средней ошибки выборки.
, то есть величина предельной ошибки равна двукратному значению средней ошибки выборки. , N-объем генеральной совокупности.
, N-объем генеральной совокупности. (для последней единицы отбора), n – объем выборочной совокупности.
(для последней единицы отбора), n – объем выборочной совокупности. . (37)
. (37)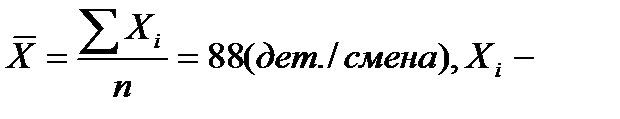 производительность труда i-го рабочего.
производительность труда i-го рабочего. .
.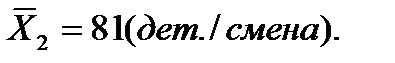
 . (38)
. (38)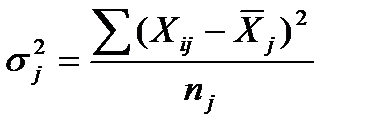 , (39)
, (39) - производительности труда i-го рабочего j-й группы;
- производительности труда i-го рабочего j-й группы; 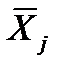 - средняя выработка рабочих j-й группы;
- средняя выработка рабочих j-й группы;  - число рабочих j-й группы. Следовательно, дисперсия первой группы:
- число рабочих j-й группы. Следовательно, дисперсия первой группы: ;
;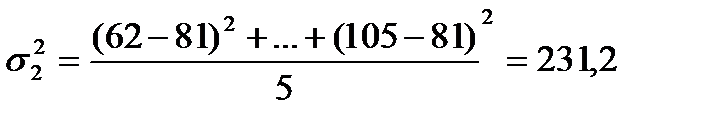 .
.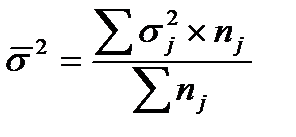 ;
; 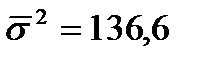 . (40)
. (40)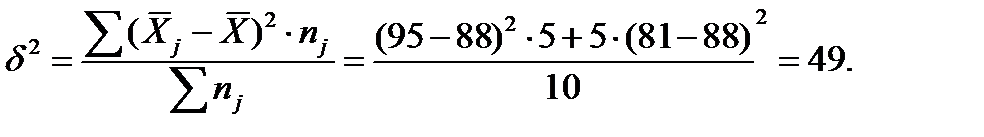
 (42)
(42)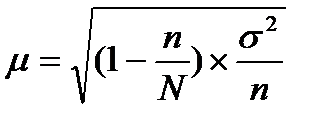 . (43)
. (43)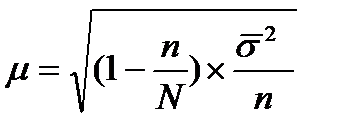 . (44)
. (44) , (45)
, (45)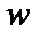 , а долю в генеральной совокупности – P.
, а долю в генеральной совокупности – P.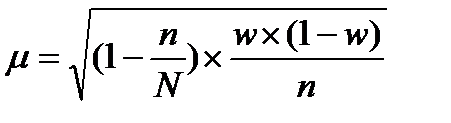 , (46)
, (46)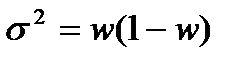 - дисперсия доли.
- дисперсия доли.


