Индекс корреляции.
Исторически первым показателем тесноты связи был парный коэффициент корреляции, предложенный К. Пирсоном. Он основан на показателе ковариации, который представляет собой среднее значение произведения отклонений индивидуальных значений результативного и факторного признаков от своих средних значений. Показатель ковариации оценивает совместное изменение двух признаков, результата и фактора:
cov =
где Показатель ковариации содержательно сложно интерпретировать. Нормированное значение показателя ковариации – это и есть показатель парной корреляции Пирсона.
или после преобразований:
где Достоинством коэффициента корреляции является то, что он имеет пределы изменения, следовательно, его величина легко может быть интерпретирована. Значения показателя изменяются от -1 до +1. Близость коэффициента к нулю свидетельствует об отсутствии корреляционной зависимости. Близость к единице – о тесной корреляционной зависимости. Знак коэффициента корреляции указывает на прямую, либо обратную зависимость. Величина конкретных значений интерпретируется следующим образом:
Парный коэффициент корреляции – симметричный показатель, т.е.
При условии справедливости нулевой гипотезы, распределение t-статистики соответствует закону распределения вероятностей Стьюдента с n-2 степенями свободы. Исходя из этого, находится табличное значение t-статистики, соответствующее заданному аналитиком уровню вероятности и полученному числу степеней свободы. Если расчетное значение t окажется больше табличного, то гипотеза об отсутствии связи должна быть отвергнута (с вероятностью ошибки В практике экономических исследований и анализа часто приходится изучать множественную корреляционную зависимость, т.е. оценивать влияние двух и более факторов на признак-результат. Теснота связи между комплексом факторов и зависимой переменной оценивается с помощью множественного коэффициента корреляции (
, (56) где Множественный коэффициент корреляции изменяется от нуля до единицы, не может быть отрицательным. Интерпретация конкретных значений множественного коэффициента корреляции аналогична интерпретации значений парного коэффициента с той только разницей, что оценивается теснота корреляционной зависимости между результативным признаком и всей совокупностью анализируемых факторов. Квадрат коэффициента корреляции (r2; При изучении множественной корреляционной зависимости рассчитываются также частные коэффициенты корреляции, характеризующие тесноту связи между результатом и одним признаком-фактором, при условии элиминирования влияния других факторов, включенных в анализ. Элиминирование выполняется путем закрепления значений факторов (кроме оцениваемого) на неизменном уровне (как правило, на среднем). При двухфакторной корреляционной зависимости рассчитывается два частных коэффициента корреляции:
Коэффициенты корреляции, в большей степени, пригодны для оценки линейной зависимости между изучаемыми признаками. Если связь нелинейная, то следует отдать предпочтение универсальному показателю, который называется корреляционное отношение ( Ø Эмпирическое, рассчитанное по данным аналитической группировки, как отношение межгрупповой дисперсии (
Ø Теоретическое, рассчитанное по результатам регрессионного анализа, как отношение факторной дисперсии (
Корреляционное отношение изменяется так же от нуля до единицы и интерпретируется аналогично коэффициенту корреляции. Квадрат корреляционного отношения ( Для понимания сути корреляционного отношения и коэффициента детерминации, следует сформулировать правило сложения дисперсий в терминах регрессионного анализа. Оно звучит так: общая дисперсия признака-результата есть сумма факторной и остаточной дисперсий:
Факторная дисперсия ( Остаточная дисперсия ( Общая дисперсияпризнака-результата ( Коэффициент детерминации ( Величина коэффициента детерминации реагирует на число факторов, включенных в уравнение регрессии. Поэтому для ответа на вопрос, какую часть дисперсии результативного признака удается объяснить в каждом конкретном случае, исходят из величины скорректированного коэффициента детерминации. Корректировка коэффициента осуществляется с учетом числа степеней свободы, т.е. с учетом объема изучаемой совокупности и числа факторов, включенных в анализ:
где Оценка корреляционной зависимости может быть также дана на основе индекса корреляции (
|

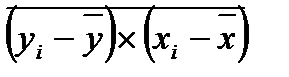 , (52)
, (52)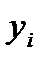 - значение признака-результата у i-й единицы совокупности;
- значение признака-результата у i-й единицы совокупности; 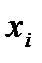 - значение признака-фактора у i-й единицы совокупности;
- значение признака-фактора у i-й единицы совокупности; 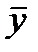 - среднее значение признака-результата;
- среднее значение признака-результата; 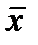 - среднее значение признака-фактора.
- среднее значение признака-фактора.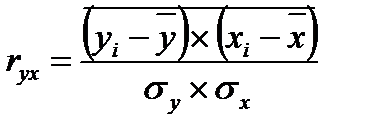 , (53)
, (53)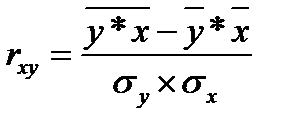 , (54)
, (54)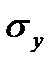 - стандартное отклонение признака-результата;
- стандартное отклонение признака-результата; 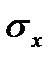 - стандартное отклонение признака-фактора.
- стандартное отклонение признака-фактора.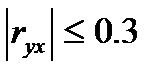 - связь практически отсутствует;
- связь практически отсутствует;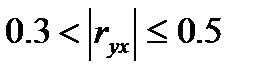 - связь заметная;
- связь заметная;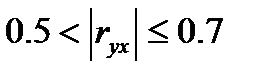 - связь умеренная;
- связь умеренная;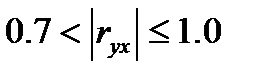 - связь тесная.
- связь тесная.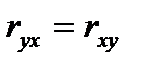 . Это означает, что высокое значение коэффициента корреляции не может свидетельствовать о наличии причинно-следственной связи, а говорит лишь о наличии параллельной вариации признаков (показателей). Что есть фактор, а что есть результат, не имеет значения. Наличие причинно-следственной связи обосновывается теоретическим анализом изучаемого объекта на основе положений экономической теории.
. Это означает, что высокое значение коэффициента корреляции не может свидетельствовать о наличии причинно-следственной связи, а говорит лишь о наличии параллельной вариации признаков (показателей). Что есть фактор, а что есть результат, не имеет значения. Наличие причинно-следственной связи обосновывается теоретическим анализом изучаемого объекта на основе положений экономической теории.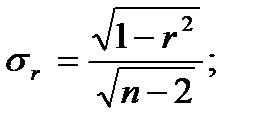
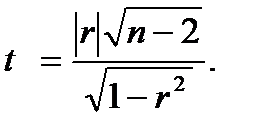
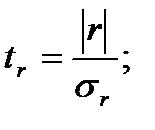 Расчет коэффициента корреляции, как и большинства статистических показателей, рассчитываемых по ограниченному объему совокупности, сопровождается оценкой его значимости (существенности). Необходимо подтвердить, что полученное значение коэффициента – не результат действия случайных факторов. Для оценки значимости рассчитывается t-статистика, как отношение оцениваемой характеристики (в данном случае - r) к ее стандартной ошибке (
Расчет коэффициента корреляции, как и большинства статистических показателей, рассчитываемых по ограниченному объему совокупности, сопровождается оценкой его значимости (существенности). Необходимо подтвердить, что полученное значение коэффициента – не результат действия случайных факторов. Для оценки значимости рассчитывается t-статистика, как отношение оцениваемой характеристики (в данном случае - r) к ее стандартной ошибке (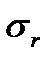 ). Иными словами, осуществляется проверка гипотезы об отсутствии корреляционной зависимости между изучаемыми переменными, т.е. предполагается, что коэффициент корреляции в генеральной совокупности равен нулю (
). Иными словами, осуществляется проверка гипотезы об отсутствии корреляционной зависимости между изучаемыми переменными, т.е. предполагается, что коэффициент корреляции в генеральной совокупности равен нулю (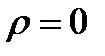 ):
): (55)
(55) =1- принятый уровень вероятности) и принята альтернативная гипотеза о значимости полученного коэффициента корреляции, т.е. о наличии статистически значимой связи между изучаемыми признаками.
=1- принятый уровень вероятности) и принята альтернативная гипотеза о значимости полученного коэффициента корреляции, т.е. о наличии статистически значимой связи между изучаемыми признаками.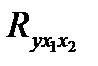 ). При двухфакторной зависимости множественный коэффициент корреляции рассчитывается следующим образом:
). При двухфакторной зависимости множественный коэффициент корреляции рассчитывается следующим образом: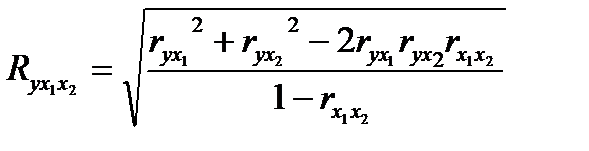
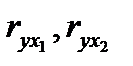 - парные коэффициенты корреляции результата и каждого из факторов,
- парные коэффициенты корреляции результата и каждого из факторов, 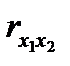 - коэффициент корреляции между факторами.
- коэффициент корреляции между факторами.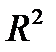 ) – это показатель, который называется коэффициентом детерминации. Он характеризует долю объясненной (факторной) дисперсии результативного признака в общей дисперсии результативного признака.
) – это показатель, который называется коэффициентом детерминации. Он характеризует долю объясненной (факторной) дисперсии результативного признака в общей дисперсии результативного признака.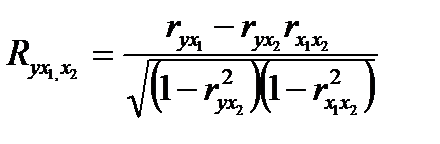 , (57)
, (57)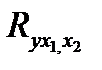 - данный частный коэффициент характеризует степень тесноты корреляционной зависимости между результатом (y) и фактором x1 при элиминировании фактора x2.
- данный частный коэффициент характеризует степень тесноты корреляционной зависимости между результатом (y) и фактором x1 при элиминировании фактора x2.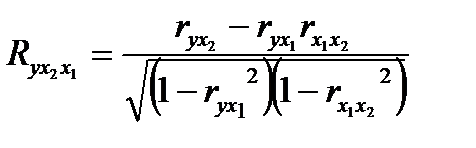 , (58)
, (58)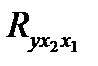 - этот коэффициент характеризует тесноту зависимости признака-результата (y) от признака- фактора x2 при элиминировании фактора x1.
- этот коэффициент характеризует тесноту зависимости признака-результата (y) от признака- фактора x2 при элиминировании фактора x1. ). Оно может быть:
). Оно может быть: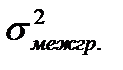 ) к общей (
) к общей ( ):
):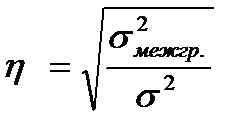 . (59)
. (59)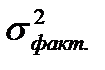 ) к общей (
) к общей ( ):
):
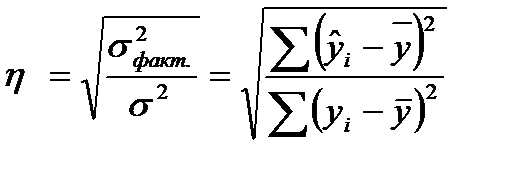 . (60)
. (60)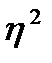 ) - коэффициента детерминации.
) - коэффициента детерминации.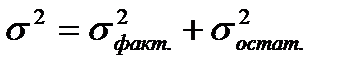 . (61)
. (61)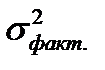 ) – это аналог межгрупповой дисперсии. Показатель характеризует вариацию признака-результата, обусловленную вариацией признаков-факторов, включенных в анализ.
) – это аналог межгрупповой дисперсии. Показатель характеризует вариацию признака-результата, обусловленную вариацией признаков-факторов, включенных в анализ.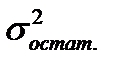 ) – аналог внутригрупповой дисперсии. Характеризует вариацию признака-результата, обусловленную вариацией факторов, не включенных в анализ, т.е. оставшихся за пределами внимания аналитика.
) – аналог внутригрупповой дисперсии. Характеризует вариацию признака-результата, обусловленную вариацией факторов, не включенных в анализ, т.е. оставшихся за пределами внимания аналитика.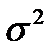 ) обусловлена вариацией всех факторов, объективно влияющих на результат (зависимую переменную).
) обусловлена вариацией всех факторов, объективно влияющих на результат (зависимую переменную).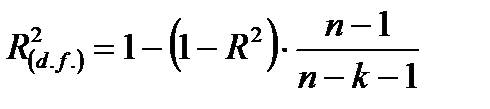 ,(62)
,(62)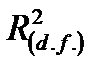 - коэффициента детерминации, скорректированный с учетом числа степеней свободы; n – объем изучаемой совокупности; k – число факторов, включенных в анализ.
- коэффициента детерминации, скорректированный с учетом числа степеней свободы; n – объем изучаемой совокупности; k – число факторов, включенных в анализ. - «ро»), который рассчитывается с использованием величины остаточной дисперсии по следующей формуле:
- «ро»), который рассчитывается с использованием величины остаточной дисперсии по следующей формуле: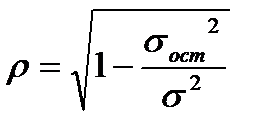 . Суть данного показателя также вытекает из правила сложения дисперсий, т.е.
. Суть данного показателя также вытекает из правила сложения дисперсий, т.е. 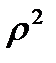 - коэффициента детерминации.
- коэффициента детерминации.


