Отбор факторов в уравнение регрессии
При построении уравнения множественной регрессии возникает задача отбора факторов, она связна с отсутствием возможности включить все факторы в уравнение (из-за ограниченного объема изучаемой совокупности) и с проблемой коллинеарности факторов. Коллинеарность – это тесная линейная зависимость между факторами, которая констатируется, если коэффициент корреляции между ними превышает значение 0,7 – 0.8. Отбор факторов в уравнении множественной регрессии может быть осуществлен на основе матрицы парных коэффициентов корреляции. Общий вид матрицы представлен в табл. 5.1. На пересечении одноименных строк и столбцов коэффициенты корреляции равны единице. Поскольку парный коэффициент корреляции – показатель симметричный, то матрица тоже симметрична относительно единичной диагонали, поэтому достаточно заполнить только один сегмент матрицы. Таблица 5.1 Матрица парных коэффициентов корреляции.
Верхняя строчка матрицы содержит парные коэффициенты, характеризующие степень тесноты связи между признаком-результатом и каждым из признаков-факторов. Остальное поле занимают коэффициенты, характеризующие степень тесноты связи между признаками-факторами. По значению этих коэффициентов делается вывод о наличии или отсутствии мультиколлинеарности. Для отбора факторов, прежде всего, рассматриваются значения коэффициентов верхней строки. Если величина коэффициента корреляции Далее просматривается остальное поле матрицы. Если, например,
2.7. Коэффициенты эластичности, β – коэффициенты Факторы, включенные в уравнении регрессии, очень часто имеют разные единицы измерения, что делает их не сопоставимыми, и не позволяет ранжировать их по силе влияния на признак-результат. С этой целью используются коэффициенты эластичности и, так называемые, β - коэффициенты. Эти показатели – относительные характеристики связи. 1. Коэффициент эластичности:
где Коэффициенты эластичности показывают, на сколько процентов изменится признак-результат при изменении признака - фактора на 1 % своей средней величины. 2. β – коэффициент:
где
|

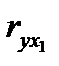
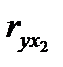
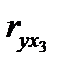
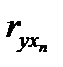

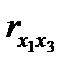

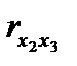
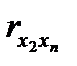
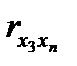

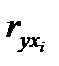 < 0.3, говорят о практическом отсутствии связи, данный фактор не имеет смысла включать в уравнение.
< 0.3, говорят о практическом отсутствии связи, данный фактор не имеет смысла включать в уравнение. , то факторы коллинеарны, между ними существует тесная линейная зависимость. Это означает, что один их факторов должен быть исключен из анализа, чтобы исключить «повторный счет» влияния каждого из факторов. Исключается тот фактор, связь которого с признаком–результатом менее тесная, т.е. коэффициент корреляции которого с результатом меньше.
, то факторы коллинеарны, между ними существует тесная линейная зависимость. Это означает, что один их факторов должен быть исключен из анализа, чтобы исключить «повторный счет» влияния каждого из факторов. Исключается тот фактор, связь которого с признаком–результатом менее тесная, т.е. коэффициент корреляции которого с результатом меньше.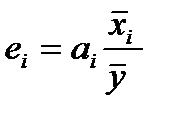 , (68)
, (68)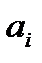 – коэффициент регрессии при i-м факторе;
– коэффициент регрессии при i-м факторе; 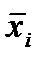 – среднее значение данного фактора;
– среднее значение данного фактора; 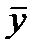 - среднее значение признака-результата.
- среднее значение признака-результата.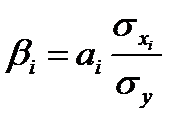 ,(69)
,(69)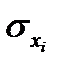 - среднее квадратическое отклонение признака-фактора;
- среднее квадратическое отклонение признака-фактора; 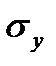 - среднее квадратическое отклонение признака-результата.
- среднее квадратическое отклонение признака-результата.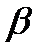 -коэффициенты показывают, на какую величину среднего квадратического отклонения изменится признак-результат при изменении признака-фактора на 1 σ.
-коэффициенты показывают, на какую величину среднего квадратического отклонения изменится признак-результат при изменении признака-фактора на 1 σ.


