Уравнение парной регрессии
Простейшим видом уравнения регрессии является уравнение парной линейной зависимости:
где y – зависимая переменная (признак-результат); x – независимая переменная (признак-фактор); В качестве уравнения регрессии могут быть использованы различные математические функции. Частое практическое применение находят уравнения линейной зависимости, параболы, гиперболы, степенной функции. Как правило, анализ начинается с оценки линейной зависимости, поскольку результаты легко поддаются содержательной интерпретации. Выбор типа уравнения связи – достаточно ответственный этап анализа. В «докомпьютерную» эпоху эта процедура занимала довольно много времени и требовала от аналитика знания свойств математических функций. В настоящее время на базе специализированных программ можно оперативно построить множество уравнений связи и на основе формальных критериев осуществить выбор лучшей модели (однако математическая грамотность аналитика не утратила своей актуальности). При построении поля корреляции, координаты точек которого соответствуют значениям зависимой и независимой переменных, выявляется тенденция связи между признаками (показателями). Если линия регрессии проходит через все точки поля корреляции, то эта свидетельствует о функциональной связи. В практике социально-экономических исследований такую картину наблюдать не приходится, поскольку присутствует статистическая зависимость. Этот факт обусловливает наличие отклонений точек поля корреляции от линии регрессии, что демонстрирует так называемые остатки или ошибки оценивания. Наличие ошибки связано с тем что: § не все факторы, влияющие на результат, учитываются в уравнении регрессии; § может быть неправильно выбрано уравнение регрессии, форма связи. Уравнение регрессии описывает изменения условного среднего значения признака-результата под влиянием конкретных значений признака-фактора, то есть это аналитическая форма тенденции зависимости между изучаемыми признаками. Построить уравнение регрессии – означает рассчитать значения его параметров. Уравнение регрессии строится на основе фактических значений анализируемых признаков. Расчет параметров, как правило, выполняется с использованием метода наименьших квадратов (МНК). Суть метода состоит в том, что удается получить такие значения параметров уравнения, при которых минимизируется сумма квадратов отклонений теоретических значений признака-результата (рассчитанных на основе уравнения регрессии), от фактических его значений:
где Задача сводится к решению задачи на экстремум, то есть необходимо найти, при каких значениях параметров функция S достигает минимума. Проводя дифференцирование, приравнивая частные производные к нулю
где Параметр Например: при изучении зависимости уровня заработной платы (у) от величины прожиточного минимума (х) получено следующее уравнение регрессии: Данное уравнение показывает тенденцию зависимости заработной платы от величины прожиточного минимума. Коэффициент Уравнение множественной регрессии – аналитическая форма зависимости признака-результата от двух или более признаков-факторов:
где § Ограниченный объем совокупности (число факторов должно в 5-6 раз (идеально в 10 раз) быть меньше объема совокупности). § Не по всем факторам имеются данные. § Не все факторы имеют количественную оценку. § Порой могут существовать факторы, о которых наука еще не знает. Коэффициент регрессии во множественном уравнении характеризует, на сколько единиц своего измерения изменится признак-результат при изменении конкретного признака-фактора на единицу, при условии элиминирования влияния всех остальных факторов, включенных в уравнение. Коэффициент регрессии во множественном уравнении регрессии не равен коэффициенту регрессии в парном уравнении регрессии (при оценке влияния одного и того же фактора), так как в уравнении множественной регрессии величина коэффициента рассчитывается в условиях элиминирования влияния ряда факторов, включенных в уравнение.
|

 , (63)
, (63)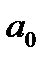 и
и 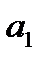 – параметры уравнения регрессии.
– параметры уравнения регрессии. ,
, , (64)
, (64)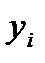 - фактическое значение признака-результата у i-й единицы совокупности;
- фактическое значение признака-результата у i-й единицы совокупности; 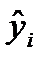 - значение признака-результата у i-й единицы совокупности, полученное по уравнению регрессии.
- значение признака-результата у i-й единицы совокупности, полученное по уравнению регрессии. и
и  , затем решая систему нормальных уравнений, находят значения параметров
, затем решая систему нормальных уравнений, находят значения параметров 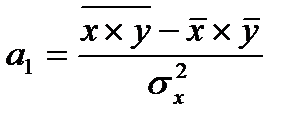 , (65)
, (65)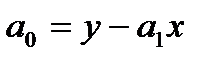 , (66)
, (66)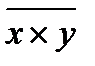 - среднее произведение значений фактора и результата;
- среднее произведение значений фактора и результата;  - среднее значение фактора;
- среднее значение фактора; 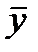 - среднее значение результата;
- среднее значение результата; 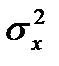 - дисперсия признака-фактора.
- дисперсия признака-фактора.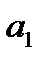 в уравнении регрессии называется коэффициентом регрессии и характеризует, на сколько единиц своего измерения изменится признак-результат при изменении признака-фактора на единицу своего измерения. Знак при коэффициенте регрессии характеризует направленность зависимости (прямая или обратная). Параметр
в уравнении регрессии называется коэффициентом регрессии и характеризует, на сколько единиц своего измерения изменится признак-результат при изменении признака-фактора на единицу своего измерения. Знак при коэффициенте регрессии характеризует направленность зависимости (прямая или обратная). Параметр  в уравнении регрессии, как правило, содержательно не интерпретируется, а характеризует лишь расположение линии регрессии на графике.
в уравнении регрессии, как правило, содержательно не интерпретируется, а характеризует лишь расположение линии регрессии на графике.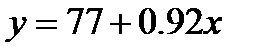 .
.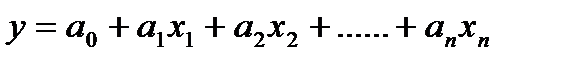 , (67)
, (67) - коэффициенты регрессии. В уравнении множественной регрессии их называют условно чистыми коэффициентами. Их можно было бы назвать чистыми коэффициентами, если бы в уравнение регрессии удалось включить все факторы, определяющие результат. Это невозможно реализовать по нескольким причинам:
- коэффициенты регрессии. В уравнении множественной регрессии их называют условно чистыми коэффициентами. Их можно было бы назвать чистыми коэффициентами, если бы в уравнение регрессии удалось включить все факторы, определяющие результат. Это невозможно реализовать по нескольким причинам:


