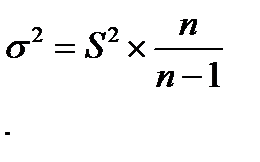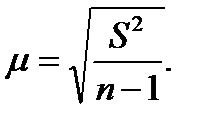Особенности малой выборки
При работе с выборками большого объема, величина ошибки выборки подчиняется нормальному закону распределения, независимо от того, какому закону подчиняется распределение единиц в генеральной совокупности. Если анализируемая выборка малого объема, то распределение ошибки выборки не подчиняется нормальному закону распределения, поэтому проблема малой выборки долго оставалась нерешенной (не была научно доказана возможность использования выборок малого объема). Она была решена английским математиком и статистом Госсетом (Стьюдентом). В 1908 году он доказал, что распределение ошибок в условиях малых выборок подчиняется особому закону распределения, который получил его имя: t-распределение Стьюдента. Распределение симметрично, как и нормальное распределение, однако ветви кривой распределения медленнее приближаются к оси абсцисс, то есть вероятность больших отклонений от средней величины в распределении Стьюдента выше, чем в нормальном распределении. Для t-распределения Стьюдента также составлена таблица, в которой вероятность связана не только с величиной t (как в таблице нормального распределения), но и с числом степеней свободы (d.f.), которое определяется, как При объеме выборки более 100 единиц значения в таблицах нормального распределения и распределения Стьюдента полностью совпадают (одинаковым значениям уровня вероятности соответствуют одинаковые значения t). При В формуле средней ошибки, в условиях малой выборки, нельзя игнорировать сомножитель
, следовательно, формула будет выглядеть:
(47)
|

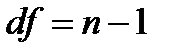 , т.е. зависит от объема совокупности.
, т.е. зависит от объема совокупности. - расхождения незначительны. Если n<30 единиц, расхождения значительные, поэтому выборка именно такого объема считается безусловно малой. При работе с выборками малых объемов, в формуле предельной ошибки выборки величина коэффициента доверия (t) берется из таблицы распределения Стьюдента, исходя из заданного уровня вероятности и соответствующего числа степеней свободы.
- расхождения незначительны. Если n<30 единиц, расхождения значительные, поэтому выборка именно такого объема считается безусловно малой. При работе с выборками малых объемов, в формуле предельной ошибки выборки величина коэффициента доверия (t) берется из таблицы распределения Стьюдента, исходя из заданного уровня вероятности и соответствующего числа степеней свободы.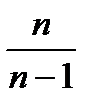 , корректирующий величину выборочной дисперсии:
, корректирующий величину выборочной дисперсии: