Визначники
Якщо матриця А квадратна, то з нею пов’язується деяке число, що називається визначником або детермінантом матриці, який скорочено позначається символами Означення. Визначником матриці другого порядку називається число Отже, Означення. Визначником матриці третього порядку називається число, що визначається за формулою
Означення. Мінором елемента матриці третього порядку називається визначник матриці другого порядку, що утворюється з даної матриці викреслюванням рядка і стовпця, на перетині яких знаходиться даний елемент. Мінор елемента Означення. Алгебраїчним доповненням елемента
де Означення. Визначником матриці n- го порядку називається число, що дорівнює сумі добутків всіх елементів першого рядка на їх алгебраїчні доповнення. Означення. Квадратна матриця А називається невиродженою, якщо її визначник не дорівнює нулю. Означення. Матриця В називається оберненою до квадратної матриці А, якщо виконується рівність АВ=ВА=Е, (1.12) де Е – одинична матриця. Отже, матриця А- 1 називається оберненою до квадратної матриці А, якщо АА- 1 = А- 1 А=Е, (1.13) де Е – одинична матриця. При яких же умовах існує обернена матриця? Введемо поняття невиродженої матриці. Означення. Квадратна матриця А називається невиродженою, якщо її визначник не дорівнює нулю. Справедлива теорема. Теорема 1. Якщо квадратна матриця має обернену матрицю, то вона невироджена.
|

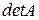 або
або 



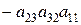 .
.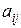 позначається символом
позначається символом  .
.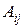 і визначається за формулою:
і визначається за формулою: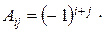
 – номер рядка,
– номер рядка,  – номер стовпця, на перетині яких знаходиться даний елемент
– номер стовпця, на перетині яких знаходиться даний елемент 


