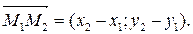Метод Гаусса
На практиці використовують метод послідовного виключення невідомих або метод Гаусса, суть якого в наступному. На першому кроці виключають одне із невідомих з цих рівнянь, крім одного. На другому кроці виключають ще одне невідоме з рівнянь, в яких вже виключене одне невідоме на першому кроці, і теж крім одного рівняння. Цей процес послідовного виключення невідомих продовжують доти, поки не дістанемо одне лінійне рівняння з одним невідомим. Це є прямий хід методу Гаусса.
Теорема Кронекера-Капеллі. Для того щоб система лінійних рівнянь була спільна, необхідно і достатньо, щоб ранг матриці системи дорівнював рангу її розширеної матриці.
Якщо при цьому ранг дорівнює числу невідомих, то система має єдине рішення, якщо він менше числа невідомих, рішень-безліч.
ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ Вектором називається напрямлений відрізок прямої. Початок вектора називається точкою прикладання вектора. Вектор, в якого початок і кінець збігаються, називається нульовим вектором або нуль-вектором, його позначають символом Вектори, що лежать на одній прямій або на паралельних прямих, називаються колінеарними. Якщо вектори а і b колінеарні, то це позначається так: а || b. Вектори, що лежать в одній площині або в паралельних площинах, називаються компланарними. Два вектори називаються рівними, якщо вони мають однакові модулі, колінеарні і однаково напрямлені. Якщо два вектори мають однакові модулі, колінеарні і протилежно напрямлені, то такі вектори називаються протилежними. Ортом вектора називається вектор, який однаково напрямлений з даним вектором і має модуль, що дорівнює одиниці. Орт вектора а позначається а ˚. Лінійні операції над векторами До цих операцій відносяться додавання і віднімання векторів та множення вектора на число. Означення. Сумою двох векторів а і b називається третій вектор с, що з’єднує початок першого вектора а з кінцем другого вектора b за умови, що початок другого вектора збігається з кінцем першого (рис. 2.3). Сума векторів а і b позначається символом с = а + b. Зауваження. Додавання трьох і більше векторів a, b, c, d, … здійснюється послідовно: спочатку додають за правилом трикутника перший вектор а з другим вектором b, потім до їх суми а + b додають третій вектор с, потім до суми а + b + с додають четвертий вектор d і т.д. Означення. Різницею векторів а і b називається такий вектор с, який в сумі з вектором b дає вектор а. Означення. Добутком вектора а на число α називається вектор b, який задовольняє такі умови: 1) модуль вектора b дорівнює добутку модуля вектора а на абсолютну величину числа α, тобто │ b │=│ α;│∙│ а │; (2.3) 2) вектор b колінеарний вектору а; 3) вектор b однаково напрямлений з вектором а, якщо число α додатне, і протилежно напрямлений з вектором а, якщо число α від’ємне. Операція множення вектора на число підпорядковане таким властивостям: 1) α; (а + b) = α а + α b – розподільний закон; 2) (α + β;) а = α а + β а – розподільний закон; 3) α;(β а) = (αβ;) а – сполучний закон; 4) 0 · а = 0; α · 0 = 0. 5) 1· а = а і (–1) · а = – а; вектор – а є протилежний вектору а. Ці властивості безпосередньо випливають з означення. Зауважимо, що дія ділення вектора на скаляр α визначається як множення вектора а на обернене число Теорема (про колінеарні вектори). Для того щоб вектори а і b були колінеарними, необхідно і достатньо, щоб виконувалась рівність b = λ а,(2.4) де λ; – деяке число. Доведення. Достатність. Якщо виконується рівність b = λ а, то з означення дії множення вектора а на число λ; (з другої умови) випливає, що b || а. Необхідність. Нехай ненульові вектори а і b колінеарні. Це означає, що ці вектори можуть відрізнятися лише довжинами, маючи однакові або протилежні напрямки. Якщо вектори а і b однаково напрямлені, то число λ = Зауваження. Якщо помножити орт вектора на модуль вектора, то дістанемо сам вектор, тобто а = звідки а 0 = Означення. Лінійною комбінацією векторів a 1, a 2,..., a n називається вектор b, що визначається рівністю b = α;1 a 1+ α;2 a 2+...+ αn a n, Означення. Вектори a 1, a 2,..., a n називаються лінійно залежними, якщо знайдуться числа α;1, α;2,..., αn, серед яких хоч би одне відмінне від нуля, такі, що виконується рівність α;1 a 1+ α;2 a 2 +...+ αn a n= 0,(2.7) тобто нульова лінійна комбінація можлива за умови, коли не всі її коефіцієнти дорівнюють нулю. Означення. Вектори a 1, a 2,..., a n називаються лінійно незалежними, якщо їх лінійна комбінація α;1 a 1 + α;2 a 2 +...+ αn a n дорівнює нульовому вектору лише в тому випадку, коли всі її коефіцієнти дорівнюють нулю, тобто за умови, що виконується рівність α;12 + α;22 +...+ αn 2 = 0. Теорема. Якщо вектори a 1, a 2,..., a n лінійно залежні, то хоч би один із них буде лінійною комбінацією решти векторів. Отже, всякі два колінеарні вектори є лінійно залежними, а всякі два неколінеарні вектори є лінійно незалежними. Теорема 3. (про розкладання вектора за двома неколінеарними векторами). Якщо вектори е 1 і е 2 неколінеарні, то будь-який компланарний з ними вектор а єдиним способом може бути розкладений за векторами е 1 і е 2. Доведення. Нехай вектори е 1 і е 2 неколінеарні і нехай задано довільний вектор а, компланарний з ними. Приведемо всі ці три вектори е1, е 2 і а до спільного початку. Спільну точку прикладання цих векторів позначимо через О, тоді згідно з означенням компланарних векторів, всі ці три вектори будуть розташовані в одній площині. Через кінець вектора а точку А проведемо прямі, паралельні з векторами е 1 і е 2, до перетину з прямими, на яких знаходяться відповідні вектори е 1 і е 2. Точки перетину, які існуватимуть, бо е 1 і е 2 неколінеарні, позначимо відповідно А 1 і А 2.
Але а = α;1 е 1 + α;2 е 2, (2.8) тобто вектор а розкладено за векторами е 1 і е 2 і це розкладання єдине, бо точки А 1 і А 2 визначаються однозначно і відповідні числа α;1 і α;2 визначаються однозначно. Теорему доведено. Якщо три ненульові вектори лінійно залежні, то вони компланарні. Означення. Кажуть, що упорядкована трійка лінійно незалежних векторів е 1, е 2, е 3 утворює базис у просторі, якщо будь-який вектор а простору можна подати у вигляді деякої лінійної комбінації векторів е 1, е 2 і е 3. Зауваження. Важливим на практиці є випадок, коли базисні вектори взаємно перпендикулярні і одиничні. Такий базис в просторі називається декартовим. Базисні вектори декартового базису позначаються так: i, j, k. Отже, | i | = | j | = | k | = 1 і i 5 .Проекція вектора на вісь Означення. Числовою віссю називається пряма, на якій вибрано початкову точку О, вказано додатний напрям та одиничний відрізок, так звану одиницю масштабу. Нехай l – деяка числова вісь і задано деякий вектор Означення. Різниця х 2 – х 1 між координатами проекцій на вісь l кінця і початку вектора а називається проекцією вектора а на вісь l і позначають символомпр l а або пр l Зауваження. Якщо через φ позначити величину кута між вектором а і віссю l, то дістанемо рівність пр l а =| а | соs φ. АВ=а А’С=|a|
Якщо кут φ; – гострий, то соs φ > 0 і пр l а є число додатне, що узгоджується з тим, що х 2 – х 1> 0; якщо ж кут φ; – тупий, то соs φ; < 0 і пр l а є число від’ємне, що відповідає тому, що х 2 – х 1< 0, бо х 2< х 1.
6. Означення. Скалярним добутком двох векторів називається число, що дорівнює добутку модулів цих векторів на косинус кута між ними. Скалярний добуток двох векторів а і b позначається символом а · b або ( Отже, за означенням скалярного добутку маємо: а · b = | а |·| b | cоsφ;, (2.22) де φ; – кут між векторами а і b або φ; = (а,^ b). – кут між векторами а і b або φ; = (а,^ b). Такий вид множення двох векторів використовується у фізиці та інших навчальних дисциплінах. Така операція використовується в механіці при визначенні роботи, що виконується сталою силою F при переміщенні точки прикладання сили на деякий вектор переміщення s. Як відомо, шукана робота А дорівнює чисельно добутку складової цієї сили на вектор переміщення FS, помноженій на модуль вектора переміщення, тобто А = FS ·| s |. Оскільки FS = | F | cosφ;, де φ; – кут між вектором сили F і вектором переміщення s, то будемо мати: А =| F |·| s | cosφ; Для того, щоб два ненульові вектори були перпендикулярні(ортогональні), необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю. 7. Означення. Векторним добутком двох векторів аіb називається вектор с, який задовольняє такі три умови: 1) модуль вектора с дорівнює добутку модулів векторів а і b на синус кута між ними; тобто | с | = | а |·| b |· sinφ;, де φ; – кут між векторами а і b; 2) вектор с перпендикулярний до кожного із векторів а і b; 3) вектор с напрямлений так, що коли дивитьсь з його кінця, то поворот від вектора а до вектора b по найкоротшому шляху повинен здійснюватися проти руху годинникової стрілки, якщо всі вектори привести до спільної точки прикладання. В цьому випадку кажуть, що трійка векторів а, b і с є правою трійкою. Векторний добуток векторів а і b позначається символом а Отже, виходячи з означення, маємо | а
Sтрикутника = 1º;. Векторний добуток колінеарних векторів дорівнює нулю. Це очевидно, бо якщо а || b, то φ; = 0 або φ; = π;, тоді sinφ; = 0. (Два вектори називаються колінеа́рними, якщо вони лежать на паралельних прямих або на одній прямій. Колінеарні вектори можуть бути співнаправленими чи протилежно направленими.Колінеарні вектори мають однаковий коефіцієнт пропорційності) 2º;. При перестановці множників векторний добуток змінює знак на протилежний, тобто а 8-9.
Отже, модуль мішаного добутку трьох некомпланарних векторів чисельно дорівнює об’єму паралелепіпеда, побудованого на цих векторах як на ребрах. З цього твердження випливає така властивість мішаного добутку трьох векторів. Три ненульові вектори а, b і с компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю. Необхідність. Якщо вектори а, b і с компланарні, то вектор d = а
Означення. Рівнянням лінії (L) на координатній площині хОу називається рівність F (x, y)=0, яку задовольняють координати будь-якої точки, що лежить на цій лінії, і не задовольняють координати жодної точки, що не лежить на цій лінії. Рівняння y=kx+b називається рівнянням прямої з кутовим коефіцієнтом. Число b – цеордината точки перетину прямоїз віссю О у. tg Канонічне рівняння прямої
Рівняння прямої, що проходить через дві задані точки
Загальне рівняння прямої Теорема. Всяке рівняння першого степеня з двома змінними Ах+Ву+С= 0, де А,В і С – задані числа, визначає на площині деяку пряму, причому вектор N = (A;B) є перпендикулярним до неї. Рівняння Ах + Ву + С = 0 називається загальним рівнянням прямої, його коефіцієнти числа А і В є координатами її нормального вектора.
|

 .
. .
. і b =
і b =  · а 0, (2.5)
· а 0, (2.5)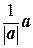 .
. Фігура ОА 1 А А 2 – паралелограм. Розглянемо вектори
Фігура ОА 1 А А 2 – паралелограм. Розглянемо вектори  і
і 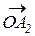 , які є сторонами паралелограма. Тоді за правилом паралелограма вектор а =
, які є сторонами паралелограма. Тоді за правилом паралелограма вектор а =  дорівнюватиме сумі векторів
дорівнюватиме сумі векторів 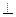 j, i
j, i  = а. Через
= а. Через  i
i  позначимо проекції на цю вісь початкової точки А і кінцевої точки В
позначимо проекції на цю вісь початкової точки А і кінцевої точки В  вектора а, які є точками перетину з віссю l площин, що проходятьчерез точки А і В перпендикулярно осі l. Нехай х 1 –координата точки
вектора а, які є точками перетину з віссю l площин, що проходятьчерез точки А і В перпендикулярно осі l. Нехай х 1 –координата точки  =
= 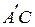 соsφ;.
соsφ;.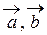 ) або (а, b).
) або (а, b).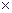 b або [ а, b ].
b або [ а, b ].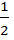 | а |·| b | =
| а |·| b | = 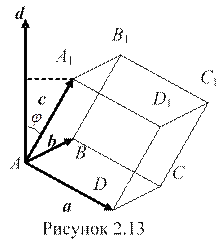 Означення. Мішаним добутком трьох векторів а, b і с називається число, що дорівнює векторному добутку перших двох векторів, помноженому скалярно на третій вектор с.
Означення. Мішаним добутком трьох векторів а, b і с називається число, що дорівнює векторному добутку перших двох векторів, помноженому скалярно на третій вектор с.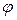 =k
=k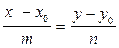 . (m,n координати параллельного вектора до вектора з початком координат у точці M0)
. (m,n координати параллельного вектора до вектора з початком координат у точці M0)