Элементы комбинаторики
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами, и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами. Размещениемk элементов из n элементов называется упорядоченная выборка (либо расположение в определённом порядке) k из этих элементов. Число размещений из n различных элементов по k элементов без повторений вычисляется по формуле Число размещений из n различных элементов по k элементов с неограниченными повторениями определяется равенством Размещения из n различных элементов по n элементов называются перестановками. Число перестановок из n различных элементов вычисляется по формуле Число перестановок с повторениями из n элементов, спецификация которых
Сочетаниемk элементов из n элементов называется выборка k из них без учёта порядка. Число сочетаний из n различных элементов по k элементов без повторений вычисляется по формуле Число сочетаний из n различных элементов по k элементов с неограниченными повторениями определяется равенством 1.1. Сколькими способами можно выбрать три различные краски из имеющихся пяти? 1.2. У одного человека есть 7 книг по математике, а у другого – 1.3. В профком избрано 9 человек. Из них нужно выбрать председателя, заместителя, культорга и секретаря. Сколькими способами это можно сделать? 1.4. На диск секретного замка нанесены 10 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим пароля? 1.5. Сколькими способами можно составить трёхцветный полосатый флаг, одна из полос которого должна быть красной, если имеется материал пяти различных цветов? 1.6. Сколькими различными способами можно выполнить групповой портрет пяти человек, если поставить: а) их в один ряд; б) трёх человек в первом ряду и двух – во втором? 1.7. Сколькими способами можно расселить девять студентов в трёх комнатах, рассчитанных на трёх человек каждая? 1.8. Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски? 1.9. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если каждая из них может повторяться несколько раз? 1.10. В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нём: а) 8 открыток; 1.11. Номера состоят из двух букв и трёх цифр. Найти число таких номеров, если используются 32 буквы русского алфавита. 1.12. Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды должны войти 3 нападающих, 2 защитника и 1 вратарь? 1.13. Сколько различных шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7 так, чтобы цифры не повторялись и крайние цифры были чётными? 1.14. Из 10 разных цветков нужно составить букет так, чтобы в него входило не менее 5 цветков. Сколько различных способов существует для составления такого букета, учитывая, что число цветков должно быть нечётным? 1.15. Сколько различных четырёхзначных чисел, делящихся на 4, можно составить из цифр 1, 2, 3, 4, 5?
1.16. В клубе велосипедистов при перерегистрации членских билетов из суеверия перестали использовать цифру 8. Сколько членов было в клубе, если известно, что использованы все трёхзначные номера, не содержащие ни одной 8? 1.17. У одного человека есть 7 книг по математике, а у другого – 9 книг. Сколькими способами они могут обменять 2 книги одного на 2 книги другого? 1.18. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если каждая цифра входит в состав числа только один раз? 1.19. В колоде 36 карт, из них 4 туза. Сколькими способами можно вынуть 6 карт так, чтобы среди них было 2 туза? 1.20. Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, 7 так, чтобы в каждом числе содержалась цифра 1 (цифры в числе не должны повторяться)?
|

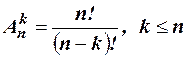 .
.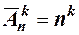 .
.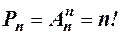 .
.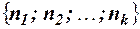 , определяется равенством
, определяется равенством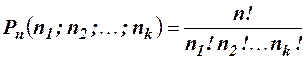 , где
, где 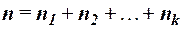 .
.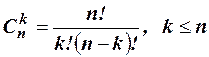 .
.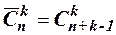 .
.


