Дискретные случайные величины. Случайная величина называется дискретной, если все её возможные значения можно перенумеровать.
Случайная величина называется дискретной, если все её возможные значения можно перенумеровать. Дискретная случайная величина обычно задаётся рядом распределения, т.е. таблицей вида
Математическое ожидание M[X] (или mx ) дискретной случайной величины X вычисляется по формуле Дисперсия D[X] дискретной случайной величины X определяется формулой
Чаще дисперсию удобнее вычислять по формуле
Среднее квадратическое отклонение s[X] случайной величины Х определяется формулой Вероятность попадания дискретной случайной величины на числовой промежуток равна сумме вероятностей значений, попадающих в данный промежуток. Функция распределения дискретной случайной величины кусочно-постоянная.
8.1. Монету бросают два раза. Случайная величина Х – число выпадений герба. Составить её ряд распределения. Найти M[X], D[X], s[X] и P { X = 0,3 }, P { 0 £ X £ 1,5 }. 8.2. Найти числовые характеристики M[X], D[X], s[X] и P { 1 £ X < 2 }, P { 2 £ X £ 4 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.
8.3. Дискретная случайная величина Х принимает три возможных значения: х 1 = 4 с вероятностью р 1 = 0,5, х 2 = 6 с вероятностью р 2 = 0,3 и х 3 с вероятностью р 3. Найти х 3 и р 3 , зная, что M[X] = 8. 8.4. Дан перечень возможных значений дискретной случайной величины Х: х 1 = 1, х 2 = 2, х 3 = 3, а также известны математические ожидания этой величины и её квадрата: M[X] = 2,3, M[X2] = 5,9. Найти вероятности, соответствующие возможным значениям Х. 8.5. Из орудия ведётся стрельба по цели до первого попадания. Вероятность попадания в цель при первом выстреле равна 0,4, при каждом следующем увеличивается на 0,1. Составить закон распределения числа истраченных снарядов, если имеется 4 снаряда. Найти числовые характеристики данной случайной величины. 8.6. Дискретная случайная величина Х принимает три возможных значения: х 1 = 1, х 2 и х 3 , причём х 1 < х 2 < х 3. Вероятности того, что Х примет значения х 1 и х 2 соответственно равны 0,3 и 0,2. Найти закон распределения величины Х, если M[X] = 2,2, D[X] = 0,76. 8.7. Найти числовые характеристики M[X], D[X], s[X] и
8.8. Найти числовые характеристики M[X], D[X], s[X] и P {
8.9. Дискретная случайная величина Х принимает два возможных значения: х 1 и х 2 , причём х 1 < х 2. Найти закон распределения величины Х, если M[X] = 1,4, D[X] = 0,24, а вероятность того, что Х примет значение х1 равна 0,6. 8.10. Производится ряд выстрелов из орудия с вероятностью попадания 0,8. Стрельба ведётся до первого попадания, но не более 4 выстрелов. Определить примерный расход снарядов на 100 подобных стрельб.
|

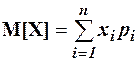 .
.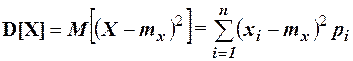 .
.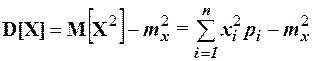 .
. .
.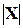 £ 1 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.
£ 1 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.


