Биномиальное распределение
Дискретная случайная величина Х называется биномиальной с параметрами n, p (n Î; N, 0 < p < 1), если её возможные значения 0, 1, 2, …, n, а их вероятности определяются по формуле Бернулли Математическое ожидание и дисперсия биноминальной случайной величины выражается через её параметры следующим образом:
10.1. Случайная величина X распределена биномиально с параметрами n = 4, p = 0,5. Найти Р { 0,5 £ X £ 2,5 }. 10.2. Вероятность выигрыша в лотерею по одному лотерейному билету равна 0,05. Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадают выигрыши, если приобретено 40 билетов. 10.3. В партии 90 % стандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырёх отобранных. 10.4. Найти дисперсию дискретной случайной величины Х – числа появления события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M[X] = 0,9. 10.5. Завод изготавливает 80 % изделий первого сорта и 20 % второго. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа изделий первого сорта в партии из 1000 отобранных случайным образом изделий.
10.6. Найти постоянную вероятность попадания в цель при каждом выстреле и число произведённых выстрелов, если среднее число попаданий равно 72, а среднее квадратическое отклонение случайной величины, характеризующей число попаданий, равно 6. 10.7. Два игральных кубика одновременно бросают два раза. Написать закон распределения случайной величины Х – числа выпадения чётного числа очков на двух игральных кубиках. 10.8. Вероятность того, что лампа остается исправной после 1000 часов работы, равна 0,2. Написать закон распределения случайной величины Х – числа неисправных ламп после 1000 часов работы из трех имеющихся. Найти числовые характеристики данной случайной величины.
|

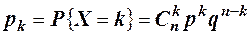 , где
, где  .
.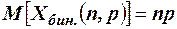 ;
; 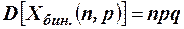 .
.


