Сложение и умножение вещественных чисел.
ГЛАВА 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА. ПОСЛЕДОВАТЕЛЬНОСТИ Вещественные числа Множества. В математике все понятия делятся на первичные и определяемые через первичные или уже известные. Основным первичным понятием математики, ее фундаментом является понятие множество. Слова «совокупность», «семейство», «система», «набор», «объединение» и т. п. являются синонимами слова «множество». Под множеством понимается некоторая совокупность объектов, которые объединены в одну группу по некоторым признакам. Примерами множеств служат: множество учащихся в аудитории; совокупность тех из них, кто получает по математике только отличные оценки; семейство звезд Большой Медведицы; множество страниц книги; множество всех целых положительных чисел и т. д. Из приведенных примеров следует, что множество может содержать конечное или бесконечное число объектов произвольной природы. Первичными понятиями являются также точка, прямая и плоскость. Для всех остальных понятий будут даны определения. Объекты, из которых состоит множество, называются его элементами или точками. Множества чаще всего обозначают большими буквами латинского алфавита, а их элементы – малыми буквами. Если x – элемент множества X, то пишут Пусть X и Y – два множества. Если X и Y состоят из одних и тех же элементов, то говорят, что они совпадают, а пишут Множество А называется подмножеством множества В, если все элементы множества А являются элементами множества В. Обозначается:
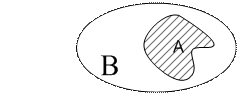
Пустое множество содержится в любом множестве, т.е. Ø Имеют место операции над множествами. Пусть А и В два множества. Объединением (суммой) множеств А и В называется такое множество S, каждый элемент которого принадлежит хотя бы одному множеству А или В. Обозначение:
. Пересечением (произведением) двух множеств А и В называется такое множество P, которое состоит из элементов множества А и элементов множества В.
Разностью двух множеств А и В называется множество D, которое состоит из элементов множества А, но не принадлежащих множеству В.
Если
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Множество с установленным порядком расположения элементов называют упорядоченным. Упорядоченное множество в отличие от просто множества записывают внутри круглых скобок. Например, из одного и того же множества Вещественные числа и их основные свойства. Понятие вещественного (действительного) числа принадлежит к основным математическим понятиям. Существуют различные подходы к определению вещественного числа (метод сечений, определение вещественного числа как бесконечной десятичной дроби и др.), однако наиболее логичным и простым является аксиоматический метод введения вещественного числа. Заметим, что все методы введения вещественного числа эквивалентны, так как ни в одном из них не устанавливается факт существования вещественного числа. Поэтому во всех случаях необходимо вводить аксиому существования вещественного числа. Поскольку же использование аксиом неизбежно, проще всего их сразу сформулировать. Множество вещественных чисел, которое обозначают Приведем основные свойства вещественных чисел, которые примем за аксиомы. Сложение и умножение вещественных чисел. Для любой пары a и b вещественных чисел определены, и притом единственным образом, два вещественных числа 1. 2. 3. 4. 5. 6. Существует единственное число 0 такое, что 7. Для любого числа a существует такое число 8. Существует единственное число 9. Для любого числа Замечание. Числа
|

 (x принадлежит X). Если x не является элементом множества X, то пишут
(x принадлежит X). Если x не является элементом множества X, то пишут 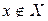 (x не принадлежит X). Если
(x не принадлежит X). Если 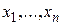 – некоторые элементы, то запись
– некоторые элементы, то запись  означает, что множество X состоит из элементов
означает, что множество X состоит из элементов  . Например, множествовсех целых положительных чисел называется множеством натуральных чисел и обозначается
. Например, множествовсех целых положительных чисел называется множеством натуральных чисел и обозначается 
 .
. .
.
 .
. А. Из определения также следует, что
А. Из определения также следует, что  .
.
 .
.
 .
. 
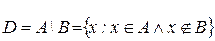
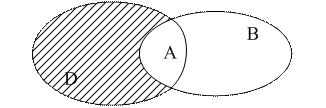
 , то множество
, то множество 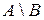 называется дополнением множества В до множества А.
называется дополнением множества В до множества А.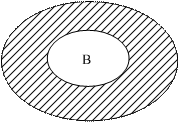
 . Пустое множество является подмножеством любого множества.
. Пустое множество является подмножеством любого множества. можно получить два упорядоченных множества:
можно получить два упорядоченных множества: 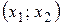 и
и  .
.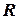 , представляет собой объединение двух множеств – рациональных чисел
, представляет собой объединение двух множеств – рациональных чисел  и иррациональных чисел. Иррациональным называется всякое вещественное число, которое не является рациональным. Всякое рациональное число является либо целым, либо его можно представить в виде конечной или периодической бесконечной десятичной дроби. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа 3 / 4 и 1 / 3 представляются соответственно следующими десятичными дробями: 0,75 и 0,333...; иррациональные числа
и иррациональных чисел. Иррациональным называется всякое вещественное число, которое не является рациональным. Всякое рациональное число является либо целым, либо его можно представить в виде конечной или периодической бесконечной десятичной дроби. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа 3 / 4 и 1 / 3 представляются соответственно следующими десятичными дробями: 0,75 и 0,333...; иррациональные числа 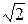 и π представляются соответственно непериодическими бесконечными десятичными дробями: 1,41421356... и 3,14159....
и π представляются соответственно непериодическими бесконечными десятичными дробями: 1,41421356... и 3,14159....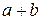 и
и  , называемые их суммой и произведением, обладающими следующими свойствами. Каковы бы ни были числа a, b и c:
, называемые их суммой и произведением, обладающими следующими свойствами. Каковы бы ни были числа a, b и c: (переместительное свойство).
(переместительное свойство).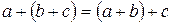 (сочетательное свойство).
(сочетательное свойство). (переместительное свойство).
(переместительное свойство). (сочетательное свойство).
(сочетательное свойство).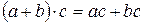 (распределительное свойство).
(распределительное свойство). для любого числа a.
для любого числа a. , что
, что 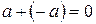 .
. такое, что для любого числа а имеет место равенство
такое, что для любого числа а имеет место равенство  .
. существует такое число
существует такое число  , что
, что 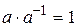 ; число
; число 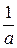 .
. , удовлетворяющее условию
, удовлетворяющее условию 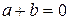 , то
, то  , откуда
, откуда  ,
,  и
и  . Получено противоречие.
. Получено противоречие.


