Числовые последовательности
Числовые последовательности встречаются уже в программе средней школы. Примерами таких последовательностей служат: • последовательность членов арифметической и геометрической • последовательность периметров правильных • последовательность Определение. Если каждому числу из множества натуральных чисел Числа Формула, задающая Примеры. 1. Дана формула общего элемента последовательности: Решение. Положив последовательно 2. Зная несколько первых элементов последовательности Решение. Знаменатели заданных элементов последовательности образуют последовательность всех нечетных натуральных чисел в степени 2. Поэтому в качестве искомой можно выбрать формулу Формула, задающая Часто используют рекуррентный способ задания последовательности
Таким образом, данное рекуррентное соотношение определяет последовательность Геометрически последовательность
Может оказаться, что одна и та же точка числовой прямой соответствует нескольким элементам последовательности, например, для последовательности с общим элементом 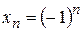 все элементы с четными номерами попадут в точку с координатой 1, а с нечетными номерами - в точку с координатой -1; для последовательности с общим элементом все элементы с четными номерами попадут в точку с координатой 1, а с нечетными номерами - в точку с координатой -1; для последовательности с общим элементом 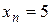 , т.е. последовательности 5, 5, 5, 5,..., все элементы попадут в одну и ту же точку с координатой 5. , т.е. последовательности 5, 5, 5, 5,..., все элементы попадут в одну и ту же точку с координатой 5.
Введем понятие арифметических действий над числовыми последовательностями. Определение. Пусть даны произвольные последовательности произведением последовательности суммой данных последовательностей называется последовательность
разностью – последовательность
произведением – последовательность
частным – последовательность
если все элементы последовательности, на которую делят, отличны от нуля. Определение. Последовательность Рекуррентное соотношение, определяющее арифметическую прогрессию, словами формулируется так: всякий член арифметической прогрессии, начиная со второго, равен предыдущему, сложенному с постоянным числом Запишем несколько первых членов арифметической прогрессии: 2; 4; 6; 8; 10; 12; 14;.... Методом математической индукции легко доказываются формула общего члена арифметической прогрессии
и формулы суммы
|

 прогрессий;
прогрессий;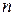 -угольников, вписанных в данную окружность;
-угольников, вписанных в данную окружность;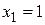

 .
. поставлено в соответствие вещественное число
поставлено в соответствие вещественное число  , то множество вещественных чисел
, то множество вещественных чисел  называется числовой последовательностью или просто последовательностью.
называется числовой последовательностью или просто последовательностью. будем называть элементами (членами) последовательности, а символ
будем называть элементами (членами) последовательности, а символ 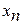 – общим элементом (членом} последовательности, а число
– общим элементом (членом} последовательности, а число  . Так, например, символ
. Так, например, символ  обозначает множество значений
обозначает множество значений 
 . Например, последовательность
. Например, последовательность  задана формулой
задана формулой 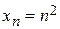 . С помощью этой формулы можно вычислить любой элемент последовательности:
. С помощью этой формулы можно вычислить любой элемент последовательности:  ,
, 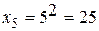 ,
, 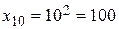 и т. д.
и т. д. . Написать пять первых элементов последовательности.
. Написать пять первых элементов последовательности.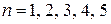 в общем элементе
в общем элементе  , получаем
, получаем  ,
, 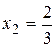 ,
,  ,
,  ,
, 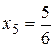 .
. ;
; 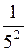 ;
; 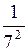 …, написать формулу общего члена последовательности.
…, написать формулу общего члена последовательности.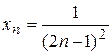 .
. , не является единственной. Так, например, последовательность –1, 1, –1,1, –1,1,... может быть задана формулой
, не является единственной. Так, например, последовательность –1, 1, –1,1, –1,1,... может быть задана формулой  или формулой
или формулой  . Однако, не всегда последовательность
. Однако, не всегда последовательность  , то последовательность запишется в виде 0, 2, 0, 2,....
, то последовательность запишется в виде 0, 2, 0, 2,.... . Вычисляя по этой формуле, получим
. Вычисляя по этой формуле, получим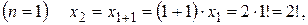
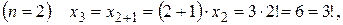
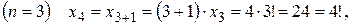

 , в которой общий элемент задается формулой
, в которой общий элемент задается формулой 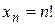 . Число n! называется факториалом и читается как n-факториал.
. Число n! называется факториалом и читается как n-факториал.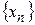 изображается на числовой прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. На рисунке изображены соответственно последовательности
изображается на числовой прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. На рисунке изображены соответственно последовательности 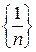 и
и 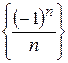 .
.
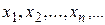 или
или 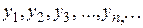 .
.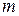 называется последовательность
называется последовательность 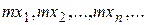 .
.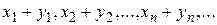 ;
; ;
;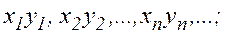
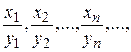
 и рекуррентным соотношением
и рекуррентным соотношением 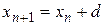 , где
, где  – постоянное число, называется арифметической прогрессией. Число
– постоянное число, называется арифметической прогрессией. Число  ,
, 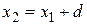 ,
, 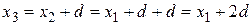 и т. д. Каждый раз прибавляем еще одно слагаемое
и т. д. Каждый раз прибавляем еще одно слагаемое 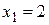 и разностью
и разностью 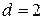 :
: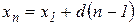
 ;
;  .
.


