Для любых двух различных вещественных чисел a и b установлено одно из отношений: 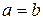 (a равно b),
(a равно b), 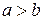 или
или 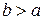 (a больше b или b больше а). Отношение = обладает свойством: если
(a больше b или b больше а). Отношение = обладает свойством: если 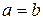 и
и  , то
, то  .
.
Вместо отношения 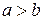 пишут также
пишут также 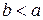 (b меньше a). Запись вида
(b меньше a). Запись вида 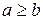 (или, что то же,
(или, что то же,  ) обозначает, что либо
) обозначает, что либо 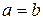 , либо
, либо 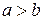 . Соотношения
. Соотношения 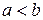 ,
,  ,
, 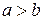 ,
, 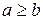 называются неравенствами. Неравенства
называются неравенствами. Неравенства 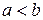 и
и 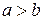 называются строгими неравенствами.
называются строгими неравенствами.
Число а, удовлетворяющее неравенству 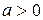 , называется положительным, а число a, удовлетворяющее неравенству
, называется положительным, а число a, удовлетворяющее неравенству  , – отрицательным.
, – отрицательным.
Отношения >;, < обладают следующими свойствами.
10. Если 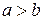 и
и 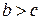 , то
, то  .
.
11. Если 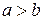 , то
, то 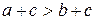 .
.
12. Если 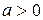 и
и 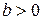 , то
, то  .
.
13.Если 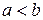 , то
, то 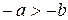 .
.
14. Если 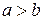 и
и  , то
, то  , т. е. неравенства одного знака можно почленно складывать.
, т. е. неравенства одного знака можно почленно складывать.

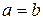 (a равно b),
(a равно b), 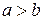 или
или 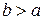 (a больше b или b больше а). Отношение = обладает свойством: если
(a больше b или b больше а). Отношение = обладает свойством: если  , то
, то  .
.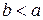 (b меньше a). Запись вида
(b меньше a). Запись вида 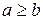 (или, что то же,
(или, что то же,  ) обозначает, что либо
) обозначает, что либо 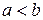 ,
,  ,
, 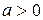 , называется положительным, а число a, удовлетворяющее неравенству
, называется положительным, а число a, удовлетворяющее неравенству  , – отрицательным.
, – отрицательным.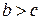 , то
, то  .
.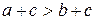 .
.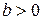 , то
, то  .
.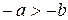 .
. , то
, то  , т. е. неравенства одного знака можно почленно складывать.
, т. е. неравенства одного знака можно почленно складывать.


