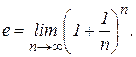Справедливы следующие свойства сходящихся последовательностей.
Теорема 1. Сходящаяся последовательность имеет только один предел. Теорема 2. Сходящаяся последовательность ограничена. . Теорема 3. Сумма (разность) двух сходящихся последовательностей
Теорема 4. Произведение сходящихся последовательностей Теорема 5. Частное двух сходящихся последовательностей
Теорема 6. Произведение бесконечно малой последовательности и ограниченной последовательности есть бесконечно малая последовательность. Теорема 7. Если последовательность Теоремы, имеют очень большое как теоретическое, так и практическое значение. Но, несмотря на свою простоту, их правильное применение вначале представляет значительную трудность. Особое внимание следует обратить на тот факт, что применение теорем требует существования конечных пределов. Покажем, какие ошибки можно сделать, если не учитывать этот факт. Рассмотрим последовательность
с другой стороны,
Получено неверное равенство Рассмотрим последовательность
с другой стороны,
Получено неверное равенство Наконец, рассмотрим последовательность
Опять получено неверное равенство Во всех рассмотренных случаях допущена грубая ошибка: неправильно применены теоремы о пределах частного, произведения и разности – последовательности Еще раз подчеркнем, что запись Такого рода неточности часто встречаются при нахождении предела последовательности, заданной в виде отношения или разности двух выражений. Например, теорему о пределе частного непосредственно применить не удается, если числитель или знаменатель не имеют конечных пределов или предел знаменателя равен нулю. В таких случаях следует предварительно преобразовать данную последовательность. Часто бывает полезно разделить числитель и знаменатель на одно и то же выражение или умножить. Этот прием будет неоднократно использован в дальнейшем. Рассмотрим теперь наиболее типичные примеры. Примеры. 1. Найти Решение. При
2. Найти Решение. В первом слагаемом в выражении, стоящем под знаком предела, применить сразу теорему о пределе частного нельзя. Поэтому, разделив сначала числитель и знаменатель на
Второе слагаемое выражения, стоящего под знаком предела, можно рассматривать как произведение ограниченной последовательности
Более компактно решение примера можно записать следующим образом:
Когда вырабатывается определенный навык, подробную запись можно сократить. 3. Найти Решение. Имеем
так как при Следовательно, на основании теоремы, имеем
4. Найти Решение. Имеем
так как при
то данная последовательность, бесконечно большая, и ее предел равен 5. Найти Решение. Здесь, хотя в числителе и стоит сумма, теорему о пределе суммы непосредственно применить нельзя, поскольку число слагаемых не конечно, а зависит от
6. Найти Решение. Так как
7. Найти Решение. Имеем
8. Найти Решение. Так как
В заключение, рассмотрим последовательность, общий член которой имеет вид
Отметим, что число e является иррациональным, оно играет важную роль в математике, в частности оно является основанием натурального логарифма, и его приближенное значение есть e =2,7182818…
|

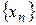 и
и 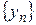 есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей
есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей  , т. е.
, т. е.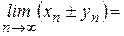
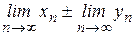 .
.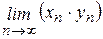
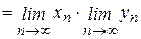 .
. .
.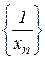 бесконечно большая, и наоборот.
бесконечно большая, и наоборот.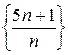 . С одной стороны,
. С одной стороны, ,
, .
. .
.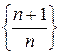 . С одной стороны,
. С одной стороны, ,
, .
. .
.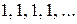 с общим элементом
с общим элементом 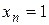 . С одной стороны,
. С одной стороны, 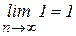 , с другой стороны,
, с другой стороны,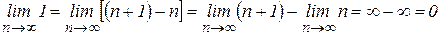 .
.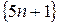 ,
, 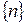 и
и  не имеют конечных пределов.
не имеют конечных пределов. не обозначает никакого числа, а является лишь выражением того, что элементы последовательности
не обозначает никакого числа, а является лишь выражением того, что элементы последовательности  нельзя обращаться как с числами и писать
нельзя обращаться как с числами и писать 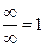 , или
, или 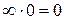 , или
, или  .
. .
.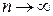 числитель и знаменатель стремятся к бесконечности и сразу применить теорему о пределе частного нельзя, так как в условии этой теоремы предполагается существование конечных пределов. Поэтому сначала преобразуем данную последовательность, разделив числитель и знаменатель на
числитель и знаменатель стремятся к бесконечности и сразу применить теорему о пределе частного нельзя, так как в условии этой теоремы предполагается существование конечных пределов. Поэтому сначала преобразуем данную последовательность, разделив числитель и знаменатель на 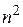 . Затем, применяя теоремы о пределе частного и о пределе суммы, найдем
. Затем, применяя теоремы о пределе частного и о пределе суммы, найдем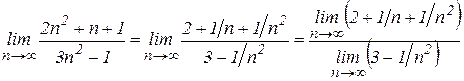
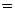
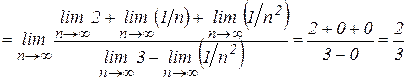 .
.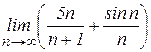 .
.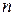 , а затем, применив теоремы о пределе частного и о пределе суммы, найдем
, а затем, применив теоремы о пределе частного и о пределе суммы, найдем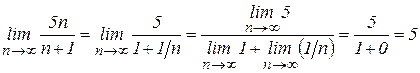 .
.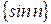
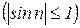 и бесконечно малой
и бесконечно малой  . Второе слагаемое является бесконечно малой последовательностью и предел ее равен нулю. Следовательно, окончательно получаем
. Второе слагаемое является бесконечно малой последовательностью и предел ее равен нулю. Следовательно, окончательно получаем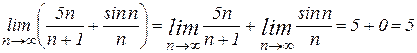 .
. 
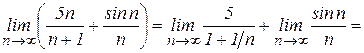
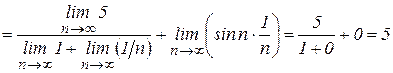 .
. .
.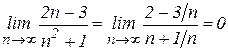 ,
,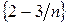
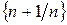 бесконечно большая (покажите это самостоятельно), а последовательность
бесконечно большая (покажите это самостоятельно), а последовательность  является бесконечно малой.
является бесконечно малой.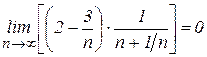 .
. .
.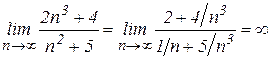 ,
,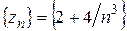 сходящаяся
сходящаяся 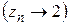 , последовательность
, последовательность 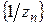 ограниченная (покажите это самостоятельно), последовательность
ограниченная (покажите это самостоятельно), последовательность 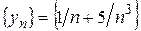 бесконечно малая (покажите это самостоятельно), а по теореме,
бесконечно малая (покажите это самостоятельно), а по теореме, ,
,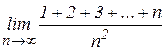 .
. есть сумма членов арифметической прогрессии с разностью
есть сумма членов арифметической прогрессии с разностью 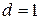 и она равна
и она равна 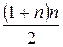 , то
, то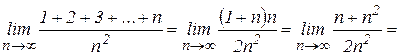
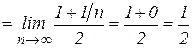 .
.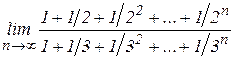 .
.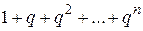 — сумма
— сумма 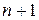 членов геометрической прогрессии со знаменателем
членов геометрической прогрессии со знаменателем  (в числителе
(в числителе 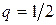 , в знаменателе
, в знаменателе  ) и она равна
) и она равна  , то
, то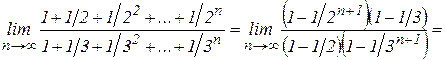
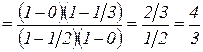 .
.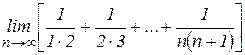 .
.
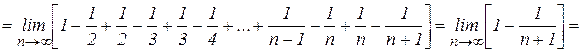
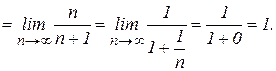
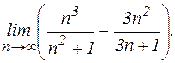
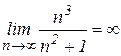 (покажите это самостоятельно) и
(покажите это самостоятельно) и 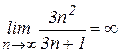 (покажите это самостоятельно), то применить непосредственно теорему о пределе разности нельзя. Поэтому сначала преобразуем выражение, стоящее под знаком предела, приведя его к общему знаменателю, и разделив числитель и знаменатель на
(покажите это самостоятельно), то применить непосредственно теорему о пределе разности нельзя. Поэтому сначала преобразуем выражение, стоящее под знаком предела, приведя его к общему знаменателю, и разделив числитель и знаменатель на 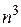 . Затем, применяя теоремы о пределе частного, произведения и разности, найдем
. Затем, применяя теоремы о пределе частного, произведения и разности, найдем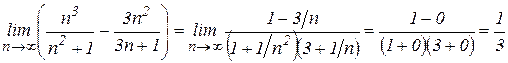 .
.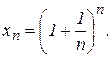 В математическом анализе доказывается, что эта последовательность возрастает, ограничена (
В математическом анализе доказывается, что эта последовательность возрастает, ограничена ( ) и имеет предел. Этот предел называют числом e. Следовательно, по определению
) и имеет предел. Этот предел называют числом e. Следовательно, по определению