Виды моделей объектов
Рассмотрим основные виды моделей линейных непрерывных стационарных динамических объектов и их взаимосвязь (действием шума e(t) пока пренебрегаем). 1. Дифференциальное уравнение. Наиболее универсальная модель, имеющая форму
где na – порядок модели (na > nb), ai и bj – постоянные коэффициенты (параметры модели), u(j)(t) и y(i)(t) – производные, соответственно, входного и выходного сигналов. 2. Передаточная функция. Данная характеристика определяется как отношение преобразования Лапласа выходного и входного сигналов, что с учетом свойств данного преобразования и вышеприведенной формулы дает
где L{●} – символ преобразования Лапласа, р – комплексная переменная (оператор Лапласа). 3. Импульсная характеристика (ИХ) w(t). Под ИХ понимается реакция предварительно возмущенного объекта (то есть объекта с нулевыми начальными условиями) на входной сигнал в виде δ-функции. 4. Переходная функция h(t). Это реакция предварительно невозмущенного объекта на входной сигнал в виде единичного скачка. Из теории автоматического управления известны следующие соотношения между этими характеристиками: L{w(t)}=W(p), w(t)=h’(t), L{h(t)}=W(p)/p (2.3)
При нулевых начальных условиях связь между выходными и входными сигналами описывается интегралом свертки:
или в операторной форме:
Y(p) = W(p)*U(p). (2.5) 5. Частотные характеристики. Частотные характеристики объекта определяются его комплексным коэффициентом передачи при подстановки вместо оператора Лапласа р комплексного аргумента jω;, который является Фурье-преобразованием ИХ. Модуль комплексного коэффициента передачи │ W(jω) │= A(ω) представляет собой, как известно, амплитудно-частотную характеристику (АЧХ) объекта с передаточной функцией W(p), а аргумент arg(W(jω))=φ(ω) – фазочастотную характеристику (ФЧХ). Графическое представление W(jω), на комплексной плоскости при изменении ω; от 0 до ∞, то есть график амплитудно-фазовой характеристики (АФХ) в полярных координатах в отечественной литературе называется годографом, а в англоязычной – диаграммой Найквиста. В теории управления часто используется логарифмическая амплитудно-частотная характеристика (ЛАЧХ), равная 20 lg │ W(jω) │. 6. Модель для переменных состояния. В 70-е годы Г. Розенброком был создан метод «размытых» частотных характеристик, предназначенный для автоматизированного проектирования систем с несколькими входами и выходами, ориентированный на использовании средств вычислительной техники и названный методом переменных состояния (МПС). В основе этого метода лежит представление дифференциальных уравнений в нормальной форме Коши, которое дополняется алгебраическими уравнениями, связывающими выходные переменные с переменными состояния:
y = C x,(2.6) где u – вектор входных воздействий; y – вектор выходных воздействий; x – вектор переменных состояния; A, B, C – матрицы коэффициентов размерности n x n, n x m, r x n соответственно; n – число переменных состояния или максимальная степень производной исходного дифференциального уравнения; m – число входов; r – число выходов. Математическим аппаратом метода переменных состояния являются матричное исчисление и вычислительные методы линейной алгебры. Метод переменных состояния содействовал значительному развитию теории управления. На языке МПС выполнена большая часть работ по оптимальному управлению, фильтрации, оцениванию. Для систем с одним входом и одним выходом уравнения переменных состояния можно сформулировать следующим образом. При выборе n координат системы (объекта) в качестве переменных ее состояния (такими координатами, например, могут быть выходной сигнал y(t) и n-1 его производных) принимаем xi, i= 1,2,…, n и данную систему можно описать следующими уравнениями для переменных состояния:
х ′(t) = A х(t) + B u(t), y(t) = C х(t) + D u(t), (2.7)
где х(t) = [ x1(t),x2(t),…,xn(t) ]T – вектор-столбец переменных состояния; A, B, C, и D при скалярных u(t) и y(t) – соответственно матрица размера n х n, векторы размера n х 1 и 1 х n и скаляр (при векторных u(t) и y(t) – матрицы соответствующих размеров). Применение при нулевых начальных условиях, к последним уравнениям преобразования Лапласа позволяет получить следующее выражение для передаточной функции:
W(p) = C(pI – A)-1 B + D, (2.8)
где I – единичная матрица. В качестве примера рассмотрим преобразование исходного дифференциального уравнения:
или в другой форме записи: y” + 2 y’ + 5 y = 3 u (2.10) в уравнения переменных состояния. Обозначим переменные состояния: x (1) = y, x (2) = y’, т.е. Перепишем уравнение (2.10) следующим образом: y” = - 2 y’ - 5 y + 3 u, (2.11) и дополним его уравнением вида: y’ = 0 y + 1 y’ + 0 u. (2.12) Тогда уравнение (2.10) можно записать следующим образом
Учитывая принятые обозначения для переменных состояния полученные уравнения приобретают вид:
Обозначим матрицы системы уравнений (2.14): A= Тогда, в конечном итоге уравнения переменных состояния примут следующий вид: х ′(t) = A х(t) + B u(t), y(t) = C х(t) + D u(t), (2.15)
Отметим, что все приведенные модели являются эквивалентными, то есть, зная любую из них, можно получить все остальные . Для объектов, функционирование которых по тем или иным причинам представляется для дискретного времени tk = kT (в данном случае T – интервал дискретизации), то есть для дискретных объектов, наиболее общим видом описания является разностное уравнение (аналог дифференциально- го): yk +a1yk-1 +... +anayk – na = b1uk + b2uk – 1 + b3uk - 2 +... + bnbuk – nb + 1, (2.16) где yk – i = y [(k – i) T ], uk – j = u [(k Связь между сигналами может быть отражена также • через дискретную свертку:
где ω – ординаты решетчатой весовой функции объекта, или, с использованием аппарата Z – преобразования:
• через дискретную передаточную функцию:
которая определяется на основании разностного уравнения после применения к обеим частям этого уравнения Z – преобразования:
Заметим, что Z – преобразованием решетчатой импульсной переходной характеристики является W(z), то есть Z { ωi } = W (z). Отметим далее, что на практике в большинстве случаев измерение непрерывных сигналов производится в дискретные моменты времени, что представляет определенное удобство при последующей обработке данных на ЭВМ. Поэтому представление непрерывных объектов дискретными моделями является актуальной задачей. Хотя такое представление может быть осуществлено с некоторой степенью приближенности. Возможны следующие способы перехода от непрерывных моделей к дискретным. 1. С применением Z – преобразования со следующей цепочкой переходов: W(p) → L- 1{ W(p) } = ω;(t) → ω;(kT) = ωk → W (z) = Z { ωk }. (2.21)
2. С заменой разности производных в дифференциальном уравнении, описывающем непрерывный объект:
(данный подход дает приемлемую точность только при малых Т). 3. С заменой Для дискретных объектов также может быть использовано описание через переменные состояния:
Xk = AXk – 1 + Buk – 1 , Yk = CXk + Duk, (2.23)
Переходную функцию и частотные характеристики – так же, как и для непрерывных сигналов. Отметим только, что множитель z – 1 = e – p T представляет собой оператор задержки.
|

 (2.1)
(2.1) , (2.2)
, (2.2)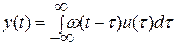 , (2.4)
, (2.4) x’ = A x + B u
x’ = A x + B u , (2.9)
, (2.9)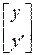 .
.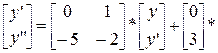 u,
u,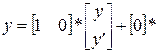 u. (2.13)
u. (2.13) . (2.14)
. (2.14)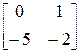 , B=
, B= 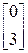 , C=
, C= 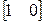 , D=
, D=  .
. – j) T ]
– j) T ]  , (2.17)
, (2.17) , где z = e pT (2.18)
, где z = e pT (2.18) , (2.19)
, (2.19)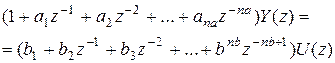 . (2.20)
. (2.20)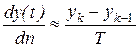 ,
,  и т.д. (2.22)
и т.д. (2.22) (приближенный способ, предложенный А. Тастиным и называемый билинейным преобразованием).
(приближенный способ, предложенный А. Тастиным и называемый билинейным преобразованием).


