Виды моделей пакета System Identification Toolbox
Основные виды моделей, используемых при идентификации объектов автоматизации, были рассмотрены ранее. Принимая во внимание это обстоятельство, и обозначая моменты дискретного времени тем же символом t, что и непрерывное время (в данном случае t = 0, 1, 3,...), приведем несколько распространенных моделей дискретных объектов, используемых в пакете System Identification Toolbox для временной области, учитывающих действие шума наблюдения. 1. Модель авторегрессии AR (AutoRegressive) – считается самым простым описанием: A(z) y(t) = u(t), где A(z) = 1 + a 1 z – 1 + a 2 z – 2 +...+ a naz – na. (3.1) 2. ARX – модель (Autoregressive with eXternal input) – более сложная модель: A (z) y(t) = B (z) u (t) + e (t), (3.2) Или в развернутом виде:
Здесь и ниже e (t) – дискретный белый шум.
3. ARMAX-модель (AutoRegressive-Moving Average wiht eXternal input – модель авторегрессии скользящего среднего):
где nk – величина задержки (запаздывания),
4. Модель «вход-выход» (в иностранной литературе такая модель называется «Output-Error», то есть «выход-ошибка», сокращенно ОЕ):
где 5. Так называемая модель Бокса-Дженкинса (BJ):
полиномы B (z), F (z), C (z) определены ранее, а полином D (z) определяется по формуле:
Данные модели можно рассматривать, как частные случаи обобщенной параметрической линейной структуры:
при этом все они допускают расширение для многомерных объектов (имеющих несколько входов и выходов). 6. Модель для переменных состояния (State-space):
где A, B, C, D – матрицы соответствующих размеров, v (t) – коррелированный белый шум наблюдений. Возможна и другая (так называемая обновленная или каноническая) форма представления данной модели:
где К – некоторая матрица (вектор столбец), е (t) – дискретный белый шум (скаляр). Следует обратить особое внимание, что в своей работе пакет System Identification Toolbox использует три внутренних вида матричного представления моделей, которые с помощью операторов и функций пакета преобразуются во все выше перечисленные виды моделей объектов: ● так называемый тета-формат (для временных моделей); ● частотный формат (для частотных моделей); ● формат нулей и полюсов.
|

 .
. .
.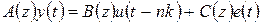 , (3.3)
, (3.3)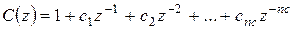 .
.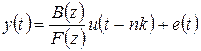 , (3.5)
, (3.5) .
.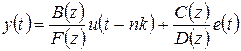 , (3.6)
, (3.6) .
. , (3.7)
, (3.7)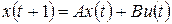 ,
, , (3.8)
, (3.8) ,
, , (3.9)
, (3.9)


