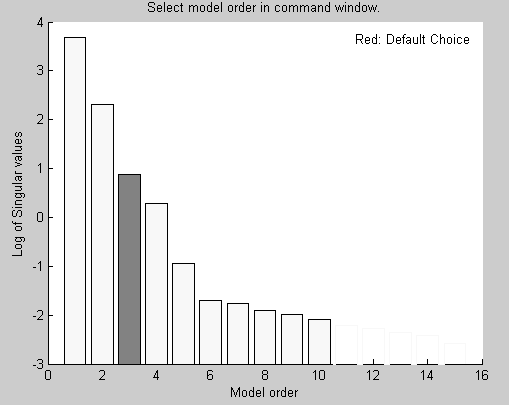
Параметрическое оценивание данныхПараметрическое оценивание экспериментальных данных проводится с целью определения параметров модели заданной структуры путем минимизации выбранного критерия качества модели (чаще всего – среднего квадрата рассогласования выходов объекта и его постулируемой модели). Для проведения параметрического оценивания массив экспериментальных данных необходимо разделить условно на две части (не обязательно равные) >> zdanv=zdan(1:500); >> zdane=zdan(501:1000). Первая часть массива данных будет использоваться для параметрического оценивания и построения модели ТОУ. Вторая часть необходима будет для верификации (проверки качества) модели, определения адекватности полученной модели и определения погрешностей идентификации. Следует напомнить, что параметрическая идентификация в пакете System Identification Toolbox MATLAB производится в дискретном виде и полученные модели, являются дискретными. В третьей главе были рассмотрены различные виды моделей ТОУ, используемых в пакете System Identification Toolbox MATLAB, которые с различной степенью достоверности описывают объект автоматизации. Для выбора наиболее приемлемой структуры и вида моделей при параметрическом оценивании экспериментальных данных в пакете System Identification Toolbox MATLAB имеются специальные функции параметрического оценивания, задания структуры модели, изменения и уточнения структуры модели и выбора структуры модели. Функция ar оценивает параметры модели авторегрессии (AR), т.е. коэффициенты полинома A(z) (см. зависимость 3.1), при моделировании скалярных временных последовательностей. Для ее использования необходимо из массива экспериментальных данных, записанных в файле dan выделить выходную переменную у с помощью команды >> y=dan.y, что равносильно команде >> y=get(dan,'y') >> dar=ar(y,4) Discrete-time IDPOLY model: A(q)y(t) = e(t) A(q) = 1 - 2.195 q^-1 + 1.656 q^-2 - 0.4167 q^-3 - 0.04415 q^-4 Estimated using AR ('fb'/'now') from data set y Loss function 0.0104048 and FPE 0.0104884 Sampling interval: 1. Полная информация о модели авторегрессии dar может быть получена с помощью команды >> present(dar) Discrete-time IDPOLY model: A(q)y(t) = e(t) A(q) = 1 - 2.195 (+-0.03165) q^-1 + 1.656 (+-0.07533) q^-2 - 0.4167 ( +-0.07542) q^-3 - 0.04415 (+-0.03174) q^-4 Estimated using AR ('fb'/'now') from data set y Loss function 0.0104048 and FPE 0.0104884 Sampling interval: 1 Created: 07-Jan-2004 08:47:27 Last modified: 07-Jan-2004 08:47:27. В информации приведены сведения о том, что модель является дискретной и для оценивания ее параметров используется прямой-обратный метод (разновидность метода наименьших квадратов), на что указывает строковая переменная 'fb' (используется по умолчанию); для построения модели используются только имеющиеся данные у, на что указывает строковая переменная 'now' (используется по умолчанию); определены: функция потерь Loss function, как остаточная сумма квадратов ошибки и так называемый теоретический информационный критерий Акейке (Akaike's Information Theoretic Criterion – AIC) FPE; интервал дискретизации Sampling interval. Для изменения параметров моделирования можно воспользоваться другой разновидностью функции ar >> [dar,refl]=ar(y,n,approach,win,maxsize,T), где n – порядок модели(число оцениваемых коэффициентов); approach – аргумент (строковая переменная) определяет метод оценивания: • 'ls' – метод наименьших квадратов; • 'yw' – метод Юла-Уокера; • 'burg' – метод Бэрга (комбинация метода наименьших квадратов с минимизацией гармонического среднего); • 'gl' – метод с использованием гармонического среднего; аргумент win (строковая переменная) используется в случае отсутствия части данных: • ‘now’ – используется по умолчанию; • 'prw’ – отсутствующие данные заменяются нулями, так что суммирование начинается с нулевого момента времени; • 'pow’ – последующие отсутствующие данные заменяются нулями, так что суммирование расширяется до момента времени N+n; • ‘ppw’ – и начальные, и отсутствующие данные заменяются нулями (используется в алгоритме Юла-Уокера); возвращаемые величины: • dar – полученная модель авторегрессии; • relf – информация о коэффициентах и функции потерь; арумент maxsize определяет максимальную размерность задачи; Т – интервал дискретизации. Следующая функция arx оценивает параметры модели ARX, представленной зависимостью 3.2: >> darx=(zdanv,[na nb nk]); где na – порядок (число коэффициентов) полинома A(z); nb – порядок полинома B(z); nk – величина задержки. Известно, что с увеличением порядка полиномов улучшается степень адекватности модели реальному объекту. Однако при этом получаются громоздкие выражения, и увеличивается время моделирования. Поэтому для нахождения оптимального порядка полиномов воспользуемся функциями выбора структуры модели. Зададим пределы изменения порядка модели: >> NN=struc(1:10,1:10,1); Вычислим функции потерь: >> v=arxstruc(zdane,zdanv,NN); Выберем наилучшую структуру порядков полиномов: >> [nn,vmod]=selstruc(v,'plot'), где 'plot' – строковая переменная, определяющая вывод графика зависимости функции потерь от числа оцениваемых коэффициентов модели (см. рис. 4.5).
Рис. 4.5. Окно выбора структуры модели
В появившемся окне столбики указывают на величину функции потерь. Подведя курсор к соответствующему столбику, в правом поле окна появятся значения порядков полиномов na, nb, nk. Воспользуемся рекомендацией, указанной в поле графика и выберем столбик, окрашенный красным цветом для оптимального значения порядков полиномов, которые указаны на рис. 4.5. Взамен строковой переменной 'plot' возможны варианты • 'log' – выводится график логарифма функции потерь; • 'aic' – график не выводится, но возвращается структура, минимизирующая так называемый теоретический информационный критерий Акейке (Akaike's Information Theoretic Criterion – AIC) FPE:
где v – значение функции потерь, d – число оцениваемых коэффициентов модели, N – объем экспериментальных данных, используемых для оценивания; • ‘mdl’ – возвращается структура, обеспечивающая минимум так называемого критерия Риссанена минимальной длины описания (Rissanen’s Minimum Description Lngth – MDL):
• при строковой переменной, равной некоторому численному значению a, выбирается структура, которая минимизирует:
• vmod – значение соответствующего критерия. Выбор наилучшей структуры порядков полиномов можно осуществить с помощью более простой команды >> nn=selstruc(v,0) nn = 7 9 1. С учетом выбранной структуры модели определим вид модели ARX:
>> darx=arx(zdanv,nn) Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + e(t) A(q) = 1 - 0.9601 q^-1 + 0.03384 q^-2 - 0.1035 q^-3 + 0.089 q^-4 - 0.02827 q^-5 + 0.1383 q^-6 - 0.06615 q^-7 B(q) = 0.0009708 q^-1 + 0.003863 q^-2 + 0.06428 q^-3 + 0.06245 q^-4 + 0.01997 q^-5 - 0.007896 q^-6 - 0.01869 q^-7 - 0.01931 q^-8 - 0.007944 q^-9 Estimated using ARX from data set zdanv Loss function 0.00139284 and FPE 0.00148493 Sampling interval: 0.1.
Следующая функция armax оценивает параметры ARMAX модели: >> darmax=armax(zdanv,[2 2 2 1]) Discrete-time IDPOLY model: A(q)y(t) = B(q)u(t) + C(q)e(t) A(q) = 1 - 1.648 q^-1 + 0.7054 q^-2 B(q) = 0.005017 q^-1 + 0.04556 q^-2 C(q) = 1 - 0.278 q^-1 - 0.4333 q^-2 Estimated using ARMAX from data set zdanv Loss function 0.00723841 and FPE 0.00741677 Sampling interval: 0.1.
Функция oe оценивает параметры ОЕ модели: >> zoe=oe(zdanv,[2 2 1]) Discrete-time IDPOLY model: y(t) = [B(q)/F(q)]u(t) + e(t) B(q) = -0.04799 q^-1 + 0.1169 q^-2 F(q) = 1 - 1.513 q^-1 + 0.5894 q^-2 Estimated using OE from data set zdanv Loss function 0.0180258 and FPE 0.0183195 Sampling interval: 0.1.
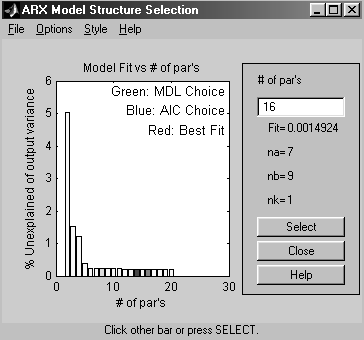
Функция bj оценивает параметры модели Бокса-Дженкинса: >> zbj=bj(zdanv,[2 2 2 2 1]) Discrete-time IDPOLY model: y(t) = [B(q)/F(q)]u(t) + [C(q)/D(q)]e(t) B(q) = 0.01242 q^-1 + 0.03574 q^-2 C(q) = 1 + 0.5362 q^-1 + 0.1415 q^-2 D(q) = 1 - 0.9029 q^-1 + 0.2424 q^-2 F(q) = 1 - 1.657 q^-1 + 0.7119 q^-2 Estimated using BJ from data set zdanv Loss function 0.00672765 and FPE 0.00695098 Sampling interval: 0.1. Функция n4sid используется для оценивания параметров моделей переменных состояния в канонической форме при произвольном числе входов и выходов: >>zn4s=n4sid(zdanv,[1:10],[1:10]), где в первых квадратных скобках задается интервал порядков модели order, и предварительные расчеты выполняются по моделям для всех заданных порядков от 1 до 10 с выводом графика, позволяющего выбрать оптимальный порядок. После этого необходимо в командной строке MATLAB набрать этот порядок и продолжить вычисление коэффициентов модели, нажав клавишу enter (см. рис. 4.6). Во вторых квадратных скобках задается так называемый дополнительный порядок, используемый алгоритмом оценивания. Должен быть больше, чем порядок, задаваемый предыдущим параметром (по умолчанию дополнительный порядок равен (1.2*order+3)). При этом выбирается оптимальный порядок без вывода соответствующего графика. Результатом выполнения команды является вывод результатов оценивания
Рис. 4.6. График для выбора оптимального порядка модели
>> zn4s=n4sid(zdanv,[1:10],[1:10]) Warning: Input arguments must be scalar. Select model order:('Return' gives default) 3 State-space model: x(t+Ts) = A x(t) + B u(t) + K e(t) y(t) = C x(t) + D u(t) + e(t) A = x1 x2 x3 x1 0.96014 -0.21598 0.062944 x2 0.24873 0.66536 0.2574 x3 -0.036067 -0.64612 0.14772 B = мощноcть x1 -0.00029117 x2 -0.012463 x3 -0.032588 C = x1 x2 x3 температура 18.093 0.078884 -0.1539 D = мощноcть температура 0 K = температура x1 0.026294 x2 -0.00982 x3 -0.076941 x(0) = x1 0 x2 0 x3 0 Estimated using N4SID from data set zdanv Loss function 0.00213802 and FPE 0.0022164 Sampling interval: 0.1. Функция pem оценивает параметры обобщенной многомерной линейной модели >> zpem=pem(zdanv) State-space model: x(t+Ts) = A x(t) + B u(t) + K e(t) y(t) = C x(t) + D u(t) + e(t)
A = x1 x2 x3 x1 0.9525 -0.20939 0.049221 x2 0.25496 0.65832 0.2538 x3 -0.038767 -0.64818 0.14259 B = мощноcть x1 -0.0002445 x2 -0.011953 x3 -0.041018 C = x1 x2 x3 температура 18.093 0.078583 -0.15352 D = мощноcть температура 0 K = температура x1 0.05191 x2 -0.006843 x3 -0.067671 x(0) = x1 0 x2 0 x3 0 Estimated using PEM from data set zdanv Loss function 0.00157651 and FPE 0.0016343 Sampling interval: 0.1.
|
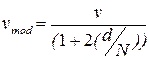, (4.1)
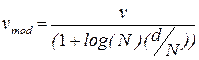; (4.2)
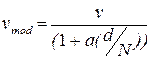; (4.3)
