Анализ модели ТОУДля анализа модели ТОУ возьмем модель zn4s, имеющею один из наилучших показателей адекватности. В разделе 4.5 были получены различные виды этой модели: • zn4s – дискретная модель тета-формата (LTI-формата)
State-space model: x(t+Ts) = A x(t) + B u(t) + K e(t) y(t) = C x(t) + D u(t) + e(t)
A = x1 x2 x3 x1 0.96014 -0.21598 0.062944 x2 0.24873 0.66536 0.2574 x3 -0.036067 -0.64612 0.14772 B = мощноcть x1 -0.00029117 x2 -0.012463 x3 -0.032588 C = x1 x2 x3 температура 18.093 0.078884 -0.1539 D = мощноcть температура 0 K = температура x1 0.026294 x2 -0.00982 x3 -0.076941 x(0) =
x1 0 x2 0 x3 0
Estimated using N4SID from data set zdanv Loss function 0.00213802 and FPE 0.0022164 Sampling interval: 0.1, где выражение Sampling interval (интервал дискретизации) указывает на то, что модель представлена в дискретном виде; • sn4s – непрерывная модель тета-формата (LTI-формата) State-space model: dx/dt = A x(t) + B u(t) + K e(t) y(t) = C x(t) + D u(t) + e(t) A = x1 x2 x3 x1 -0.19842 -1.6567 1.7776 x2 2.6343 -1.0547 5.106 x3 1.474 -13.427 -12.397 B = мощноcть x1 0.02622 x2 -0.022958 x3 -0.65355 C = x1 x2 x3 температура 18.093 0.078884 -0.1539 D = мощноcть температура 0 K = температура x1 0.34674 x2 0.10592 x3 -1.4143 x(0) = x1 0 x2 0 x3 0 Estimated using N4SID from data set zdanv Loss function 0.00213802 and FPE 0.0022164; Как видно в представленных моделях значения коэффициентов матриц A, B, C, D, K различны. Это объясняется тем, что для непрерывной модели произведено Z-преобразование с целью получения дискретной модели; • zzn4s – дискретная модель в виде передаточной функции
• sysn4s – непрерывная модель в виде передаточной функции
Следует напомнить, что приведенные виды являются одной и той же моделью, записанной в разных формах и форматах. Проанализируем динамические характеристики модели. Построим переходную характеристику ТОУ для дискретной и непрерывной моделей и определим основные показатели переходного процесса. Для этого можно воспользоваться командой step(zn4s,sn4s), либо командой plot(zn4s,sn4s). Различие заключается в том, что в последнем случае представляется возможность использовать все достоинства LTI view (см. рис. 4.21).
Рис. 4.21. Графики переходных процессов модели zn4s На графиках переходных процессов ступенчатой линией представлен переходной процесс дискретной модели, а сплошной линией – непрерывной модели. Кроме того, в поле графика указаны основные характеристики переходного процесса: • время нарастания переходного процесса (Rise time) – 0,913 с для непрерывной модели и 0,9 с для дискретной модели; • время регулирования (Setting time) – 1,9 с для обоих моделей; • установившееся значение выходной координаты (Final value) – 0,948 для обоих моделей. Для построения импульсной характеристики моделей необходимо воспользоваться командой impulse(zn4s,sn4s), либо, щелкнув правой кнопкой мыши в поле графика LTI view, выбрать опцию Plot Types ►Impulse (см. рис. 4.22).
Рис. 4.22. Графики импульсной характеристики
Основными характеристиками модели ТОУ при подаче на вход единичного импульсного воздействия являются: • пиковая амплитуда (Peak amplitude) составляет для дискретной модели 0,14, а для непрерывной – 1,41. • время регулирования составляет для дискретной модели 2,2 с, а для непрерывной модели – 2,1 с. Определим статический коэффициент усиления модели ТОУ с помощью команды >> k=dcgain(sysn4s) k = 0.9476. Определим частотные характеристики моделей с помощью команды bode (zn4s,sn4s) либо, щелкнув правой кнопкой мыши в поле графика LTI view, выбрать опцию Plot Types ► Bode (см. рис. 4.23).
Рис. 4.23. Частотные характеристики моделей
На графиках частотных характеристик указаны значения запасов устойчивости по амплитуде (Gain Margin), которые для дискретной модели составляет 9,3 dB, а для непрерывной модели – 10,5 dB. Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команд: >> [Gm,Pm,Wcg,Wcp]=margin(sysn4s) – для непрерывной модели:
Gm = 3.3642 Pm = Inf Wcg = 6.1977 Wcp = NaN. >> [Gm,Pm,Wcg,Wcp]=margin(zzn4s) – для дискретной модели: Gm = 2.9158 Pm = Inf Wcg = 5.4941 Wcp = NaN, где Gm – запас устойчивости по амплитуде в натуральных величинах на частоте Wcg, Pm – запас устойчивости по фазе на частоте Wcp. Для определения запасов устойчивости в логарифмическом масштабе необходимо выполнить следующие операции: >> Gmlog=20*log10(Gm) – для дискретной модели: Gmlog = 9.2951 >> Gmlog=20*log10(Gm) – для непрерывной модели: Gmlog = 10.5377. Как видно, определение запасов устойчивости последним способом позволяет значительно точнее вычислять эти значения, чем на графиках частотных характеристик. Анализ частотных характеристик показывает, что модели zzn4s и sysn4s являются устойчивыми с соответствующими запасами устойчивости по амплитуде. Запас устойчивости по фазе равен бесконечности. Этот вывод подтверждается так же комплексной амплитудно-фазовой характеристикой АФХ, которая в зарубежной литературе называется диаграммой Найквиста (см. рис. 4.24), так как годограф АФХ не пресекает точку комплексной плоскости с координатами –1, j0. Для построения АФХ необходимо воспользоваться командой nyquist(zzn4s,sysn4s), либо, щелкнув правой кнопкой мыши в поле графика LTI view, выбрать опцию Plot Types ► Nyquist. Определить устойчивость моделей можно с помощью карты нулей и полюсов по расположению нулей моделей относительно окружности с единичным радиусом на комплексной плоскости, как это было показано на рис. 4.7. Построить карту нулей и полюсов моделей можно так же с помощью команды pzmap(zzn4s,sysn4s), либо – pzmap(zn4s,sn4s).
Рис. 4.23. Годограф АФХ с указанием значений запасов устойчивости для непрерывной и дискретной моделей
Следует напомнить, что модель объекта автоматизации рассматривается нами в виде, показанном на рис. 1.1, при этом выходной параметр объекта автоматизации (в нашем случае температура) y (t) складывается из двух составляющих: теоретический выход объекта y’ (t) и аддитивная помеха e (t), вызванная влиянием внешних факторов на объект автоматизации. Последняя составляющая является чисто случайной величиной и характеризуется статистическими параметрами. В ходе идентификации в разделе 4.6 нами были получены зависимости, определяющие составляющую e (t) и корреляционные зависимости между e (t) и выходом объекта y’ (t). Для наглядности построим график изменения e (t) и определим основные статистические характеристики помехи с помощь команды plot (e) (см. рис.4.24). Для получения статистических характеристик необходимо в строке меню графика в позиции Tools выбрать опцию Data statistics. Результатом выполнения команды явится окно, в котором будут указаны основные статистические характеристики случайного процесса изменения во времени e (t)
Рис. 4.24. График аддитивной помехи e (t)
Рис. 4.25. Статистические характеристики e (t)
(см. рис. 4.25), к которым относятся: • min и max – минимальное и максимальное значения помехи. Для нашего случая – 0,1976 и 0,3563 соответственно; • mean – арифметическое среднее значение (0,09945); • median – медиана процесса (0,09806); • std – среднеквадратическое отклонение (0,08177); • range – диапазон изменения помехи от минимального до максимального значения (0,5242). Во всех случаях размерность аддитивной помехи такая же, как и выходная величина объекта автоматизации – оС. Полученные статистические характеристики помехи могут быть полезны в дальнейшем при синтезе системы автоматического регулирования температуры теплового объекта автоматизации. Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область)? До второй половины девятнадцатого столетия проблема управляемости – проблема установления обладания объектом свойством управляемости решалась чисто интуитивно на основе инженерных знаний и опыта. В настоящее время, с развитием метода переменных состояния стало возможным строгое определение свойства управляемости и установление критерия управляемости. Решение проблемы управляемости основано на анализе уравнений переменных состояния вида 3.8 или 3.9 и формулируется следующим образом: объект называется вполне управляемым, если выбором управляющего воздействия u(t) на интервале времени [t0, tk] можно перевести его из любого начального состояния y(t0) в произвольное заранее заданное конечное состояние y(tk). Критерием управляемости линейных стационарных объектов является условие: для того чтобы объект был вполне управляем, необходимо и достаточно, чтобы ранг матрицы управляемости MU = (B AB A2B … An-1B) (4.10) равнялся размерности вектора состояний n rang MU = n. (4.11) В пакете Control System Toolbox имеется функция ctrb, формирующая матрицу управляемости в пространстве состояний. Для того, чтобы воспользоваться этой функцией необходимо вычислить матрицы A, B, C, D с помощью команды:
>> [A,B,C,D]=ssdata(sn4s)
A = -0.1984 -1.6567 1.7776 2.6343 -1.0547 5.1060 1.4740 -13.4267 -12.3967 B = 0.0262 -0.0230 -0.6535 C = 18.0931 0.0789 -0.1539 D = 0. Следует обратить внимание, что для расчета матриц используется непрерывная модель, так как дискретная модель имеет другие значения, а в критерии управляемости используются матрицы линейных непрерывных стационарных объектов. Вычислим матрицу управляемости: >> Mu=ctrb(A,B) Mu = 0.0262 -1.1289 20.6164 -0.0230 -3.2437 43.5862 -0.6535 8.4487 -62.8481. Определим ранг матрицы управляемости: >> n=rank(Mu) n = 3. Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и B равна трем и ранг матрицы управляемости MU также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне управляемым, т.е. для него имеется такое управляющее воздействие u(t), которое способно перевести на интервале времени [ t0, tk ] объект из любого начального состояния y(t0) в произвольное заранее заданное конечное состояние y(tk). При синтезе оптимальных систем с обратной связью сами управления получаются как функции от фазовых координат. В общем случае фазовые координаты являются абстрактными величинами и не могут быть исследованы. Поддается измерению (наблюдению) вектор y = (y1, …, yk)T, который обычно называют выходным вектором или выходной переменной, а его координаты – выходными величинами. Выходная переменная функционально связана с фазовыми координатами, и для реализации управления с обратной связью необходимо определить фазовые координаты по измеренным значениям выходной переменной. В связи с этим возникает проблема наблюдаемости, заключающаяся в установлении возможности состояния определения состояния объекта (фазового вектора) по измеренным значениям выходной переменной на некотором интервале. Решение проблемы наблюдаемости основано на анализе уравнений переменных состояния вида 3.8 или 3.9 и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(t1) на выходе объекта, на интервале времени [ t 0, t 1] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта. Критерием наблюдаемости линейных стационарных объектов является условие: для того, чтобы объект был вполне наблюдаемым, необходимо и достаточно, чтобы ранг матрицы наблюдаемости МY = (CT ATCT (AT)2CT … (AT)n-1C) (4.12) равнялся размерности вектора состояния n = rang MY. (4.13) Определим матрицу наблюдаемости и ее ранг с помощью функций пакета Control System Toolbox: >> My=obsv(A,C) My = 18.0931 0.0789 -0.1539 -3.6091 -27.9915 34.4730 -22.2084 -427.3557 -576.6903 >> n=rank(My) n = 3. Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и С равна трем и ранг матрицы наблюдаемости MY также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне наблюдаемым, т.е. для него всегда можно определить по значениям выходной величины y(t) вектор переменных состояния, необходимый для синтеза системы управления.
|
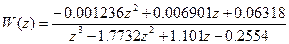; (4.8)
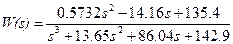. (4.9)
