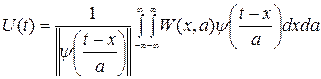Дискретные преобразования Фурье (ДПФ) и обратные ДПФ.
Комплексная форма:
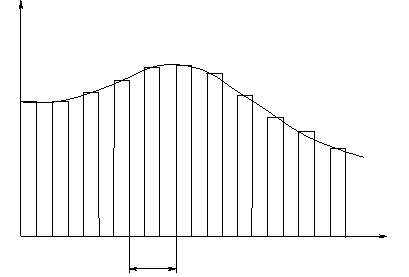
Модулированная импульсная последовательность (МИП):
Математическая модель МИП получается из динамического представления:
Дискретизируя, получим Пусть дискретный сигнал состоит из N -отсчетов на отрезке [0,Т], т.е. задан отсчетами x0 , x1, …, xN -1; Дальнейший анализ состоит в том, чтобы продолжить периодически на числовой оси с периодом Т дискретизировать. Тогда к такому сигналу можно применить комплексную форму ряда Фурье, только частоту ω1 заменим на
Коэффициенты спектра ДПФ: Восстановление МИП (обратное ДПФ): Последние 2 выражения – это аналоги преобразований (*) и (**). Недостаток же состоит в том, что надо вычислить много точек N 2. Поэтому существует алгоритм «быстрого» преобразования Фурье (БПФ) в Matlab (FFT). Идея: исходная последовательность дискретных отсчетов делится на две подпоследовательности (например четную и нечетную). Каждая из них делится еще на две подпоследовательности, и так до конца, пока не останется пара отсчетов. Для них определяются коэффициенты ряда Фурье, а затем по ним восстанавливаются коэффициенты более высших подпоследовательностей по подмеченным простым закономерностям:
В итоге, число вычислений =
Частотно – временной анадиз (Вейвлет-преобразования)
Недостаток преобразований Фурье в том, что при анализе процессов с локальными изменениями он является громоздким. Поэтому был разработан «оконный» метод анализа, который использует другой базис, называемый вейвлетами. При этом в нужную область процессов «подтягивается» вейвлет (его копии) и из этих вейвлетов и конструируется локальное изменение процессов. Требования к вейвлету: 1) Он должен осциллировать в окрестности определенной точкой и резко убывать при удалении от неё, а площадь под ним равна нулю.
2) Энергия вейвлета должна быть конечной
Примеры вейвлетов а) вейвлет Добоши б) вейвлет Морле в) «Мексиканская шляпа» в) это вторая производная функции Гаусса
Вейвлет-преобразование это аналог преобразования Фурье, но не прямой аналог. По Фурье ядром преобразования является экспонента
А в вейвлет-преобразованиях ядром является вейвлет, смещенный по оси времени в нужную точку процесса, а также растянутый или сжатый в a раз.
x – размерность времени, с. a – размерность периода, с.
Вейвлет-преобразования бывают: 1-аналоговые; 2-дискретные.
Коэффициенты (28) показывают, какие характеристики частоты В (28) содержится и частотная (как в Фурье) и временная информация, поэтому вейвлеты могут быть изображены в пространстве.
Восстановление сигнала по вейвлет коэффициентам проводится:
|

 , где Сn – коэффициенты ряда Фурье. (*)
, где Сn – коэффициенты ряда Фурье. (*) . (**)
. (**)
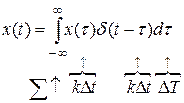
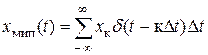 .
.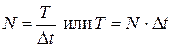
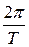 или
или 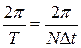 . Тогда коэффициенты ряда Фурье:
. Тогда коэффициенты ряда Фурье:
 .
.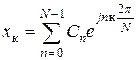 .
. .
.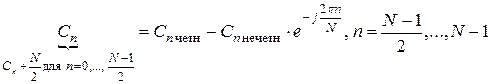 .
.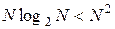 .
. Wavelet – маленькая волна.
Wavelet – маленькая волна.
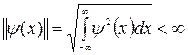
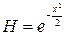


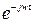
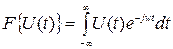
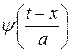
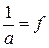 - частота.
- частота.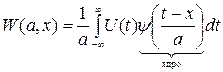 (28)
(28)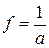 содержатся в сигнале в окрестности точки X, куда подтянули вейвлет.
содержатся в сигнале в окрестности точки X, куда подтянули вейвлет.