Площадь треугольника.
ТРЕУГОЛЬНИК.
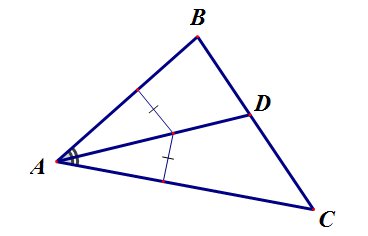
Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
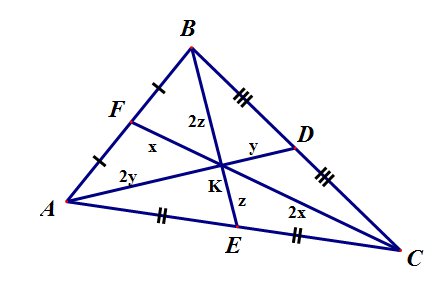
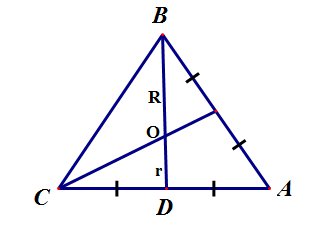
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший – радиусу описанной окружности.
Длина медианы произвольного треугольника вычисляется по формуле: Биссектриса треугольника – это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:
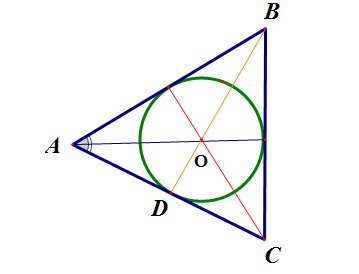
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
Все точки биссектрисы угла равноудалены от сторон угла.
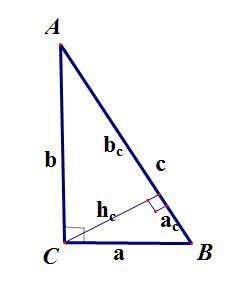
Высота треугольника – это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. Чтобы найти высоту треугольника, проведенную к стороне
Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.
Радиус описанной окружности треугольника можно найти по таким формулам:
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов:
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
Прямоугольный треугольник – это треугольник, один из углов которого равен 90°. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
Радиус окружности, вписанной в прямоугольный треугольник, равен
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Определение синуса, косинуса, тангенса и котангенса прямоугольного треугольника я подробно рассматривала здесь. Соотношение элементов в прямоугольном треугольнике: Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:
Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:
|

 , здесь
, здесь  – произвольная сторона треугольника,
– произвольная сторона треугольника, 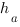 – высота, опущенная на эту сторону.
– высота, опущенная на эту сторону.
 , здесь
, здесь  и
и 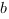 – произвольные стороны треугольника,
– произвольные стороны треугольника,  – угол между этими сторонами.
– угол между этими сторонами.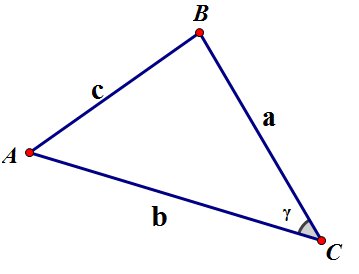
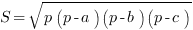 - формула Герона. Здесь
- формула Герона. Здесь 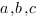 – длины сторон треугольника,
– длины сторон треугольника, 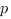 - полупериметр треугольника,
- полупериметр треугольника, 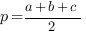
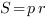 , здесь
, здесь  – радиус вписанной окружности.
– радиус вписанной окружности.
 , здесь
, здесь  – длины сторон треугольника,
– длины сторон треугольника,  – радиус описанной окружности.
– радиус описанной окружности.
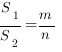

 , здесь
, здесь 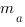 – медиана, проведенная к стороне
– медиана, проведенная к стороне 


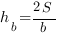

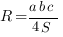 – здесь
– здесь  – площадь треугольника.
– площадь треугольника.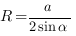 , где
, где  – противолежащий угол. (Эта формула вытекает из теоремы синусов).
– противолежащий угол. (Эта формула вытекает из теоремы синусов).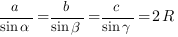


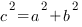
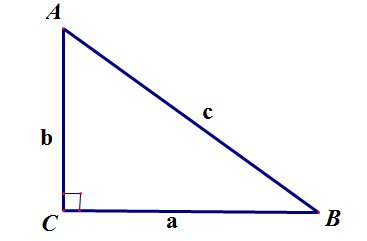
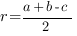 , здесь
, здесь 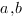 – катеты,
– катеты,  – гипотенуза:
– гипотенуза:


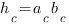
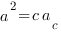
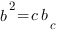
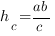 :
: