Устойчивость решения при изменении удельной прибыли.
В реальных условиях удельная прибыль от производства продукции
Тесты 1. Какая задача является задачей линейного программирования: а) управления запасами; б) составление диеты; в) формирование календарного плана реализации проекта. 2. Тривиальными ограничениями задачи линейного программирования называются условия: а) ограниченности и монотонности целевой функции; б) не отрицательности всех переменных; в) не пустоты допустимого множества. 3. Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то: а) допустимое множество не ограничено; б) оптимальное решение не существует; в) существует хотя бы одно оптимальное решение. 4. Линейное программирование – это раздел исследования операций, изучающий: а) методы нахождения экстремума линейной функции; б) методы нахождения экстремума линейной функции с линейными ограничениями; в) методы нахождения экстремума произвольной функции с линейными ограничениями. 5. Область допустимых решений задачи линейного программирования определяется: а) системой линейных неравенств и условиями неотрицательности переменных; б) системой уравнений общего вида и условиями неотрицательности переменных; в) системой линейных уравнений и условиями неотрицательности переменных. 6. Симплекс-метод решения задачи ЛП – это: а) метод целенаправленного перебора допустимых базисных решений в направлении оптимального значения целевой функции; б) метод последовательного перебора допустимых базисных решений задачи ЛП; в) метод нахождения допустимых базисных решений задачи ЛП. 7. Где довольно часто встречаются на практике задачи линейного программирования? а) при решении проблем, связанных с распределением ресурсов; б) при планировании производства; в) при организации работы транспорта; г) содержание п. а, б, в. д) содержание п. а, б. 8. Объективно-обусловленные оценки ресурсов показывают: а) избытки несущественных ресурсов; б) на сколько увеличится прибыль, если ресурс увеличить на единицу; в) оптовую цену. 9. Соотношение устойчивости показывает: а) при каких диапазонах изменения коэффициентов целевой функции оптимальное решение сохранится; б) отношение коэффициентов целевой функции к оптимальным объемам производства; в) отношение коэффициентов целевой функции к нормативной потребности в ресурсах. 10. Какая задача не описывается моделью линейного программирования: а) управление запасами на складе; б) Задача использования ресурсов; в) Задача оптимального использования удобрений; г) Задача составления диеты; д) Задача о раскрое материалов.
Ответы к тестам
Контрольные вопросы 1. В задаче составления плана производства дать постановку экономической задачи. 2. Для задачи составления плана производства описать переменные и параметры задачи. 3. Для задачи составления плана производства описать основные экономические условия. 4. Для задачи составления плана производства сформулировать ограничения задачи. 5. Что принимается в качестве целевой функции в задаче составления плана производства? 6. Дать экономический смысл точного равенства в ограничении задачи составления плана производства. 7. Экономический смысл оптимального решения в задаче составления плана производства. 8. Экономический смысл строгого неравенства в ограничении задачи составления плана производства. 9. Для задачи составления плана производства записать двойственную задачу. 10. В двойственной задаче для задачи составления плана производства привести экономический смысл целевой функции. 11. В двойственной задаче для задачи составления плана производства привести экономический смысл ограничений. 12. В двойственной задаче для задачи составления плана производства привести экономический смысл переменных. 13. Проанализировать изменение целевой функции в линейной модели производства при изменении цен реализации продукции. 14. Проанализировать изменение целевой функции в линейной модели производства при изменении запаса дефицитного ресурса. 15. Проанализировать изменение целевой функции в линейной модели производства при изменении запаса недефицитного ресурса. 16. Привести экономический смысл связи целевых функций прямой и двойственной задач в линейной модели производства. 17. Указать отличие линейных экономических моделей от нелинейных. 18. Привести примеры задач линейного программирования. 19. Как поставить задачу линейного программирования? 20. Каковы особенности графического метода решения задачи линейного программирования: построение области допустимых значений, нахождение оптимальной точки или прямой. 21. Указать особенности двойственной задачи линейного программирования.
|

 и
и  может меняться. Поэтому составим соотношение устойчивости, т.е. найдем пределы, до которых может отклоняться нормаль целевой функции, чтобы решение системы оставалось в точке В.. Руководствуясь правилом, что у больших углов больший тангенс, составим соотношение устойчивости:
может меняться. Поэтому составим соотношение устойчивости, т.е. найдем пределы, до которых может отклоняться нормаль целевой функции, чтобы решение системы оставалось в точке В.. Руководствуясь правилом, что у больших углов больший тангенс, составим соотношение устойчивости: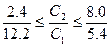 ;
;  ;
; 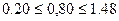 .
.


