ТЕМА 2.7. СОСТЯЗАТЕЛЬНЫЕ ЗАДАЧИ
2.7.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИГР 196 2.7.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИГРЫ 199 2.7.3. ИГРЫ С ПРИРОДОЙ 204 2.7.4. БИМАТРИЧНЫЕ ИГРЫ 214 2.7.5. ПОНЯТИЕ КОАЛИЦИОННЫХ ИГР 226 2.7.6. ПРАКТИЧЕСКИЙ БЛОК 227 2.7.7 САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ 235 Основные понятия теории игр. Решение многих экономических задач для индивидуального участника экономических отношений (производителя, потребителя, продавца, покупателя и т.п.) сводится к максимизации полезности при условии сбалансированности своего бюджета. Задачи часто выражаются альтернативно, как, например, максимизация выпуска продукции при заданных издержках или минимизация издержек при данном выпуске. Каждый индивидуум старается достичь максимума своей прибыли, и на его действия не оказывают влияния действия других индивидуумов. Однако в других экономических ситуациях возникают конфликты интересов, которые должны быть разрешены. Конфликты интересов возникают между продавцом и покупателем, между конкурирующими продавцами (производителями). Более сложные ситуации возникают, если образуются коалиции лиц, участвующих в столкновении интересов, например, в том случае, когда ставки заработной платы определяются союзами рабочих и предпринимателей. Решение таких проблем поднимает более сложные вопросы о стратегиях поведения участников, и соответствующие математические формулировки этих проблем и методы их решения составляют теорию игр. Игра – это совокупность правил и процедур, которым подчиняются ее участники для достижения своей цели. Каждый участник (игрок) имеет множество возможных ходов, выбрать один из них – значит сделать ход. Партия – это последовательность ходов, сделанных в соответствии с правилами игры и приводящих ее к конечному состоянию. Во многих играх достижение цели сопровождается каким-нибудь выигрышем. Выигрыш в игре будем рассматривать в количественном выражении, причем отрицательное значение выигрыша интерпретируется как проигрыш. Игра с нулевой суммой – это такая игра, в которой сумма выигрышей участников равна нулю. Стратегия – это установленный игроком метод выбора решения при каждом ходе в течение игры. Будем рассматривать конечную игру, то есть игру с конечным числом ходов и конечным числом стратегий. Платежная матрица – это таблица, которая определяет, какие выигрыши должны быть получены игроками после завершения игры. Рассмотрим игру двух лиц с нулевой суммой. Обозначим игроков А и В, и пусть А имеет n вариантов хода, а В имеет m вариантов. Пусть игра заключается в том, что игроки делают по одному ходу и А выигрывает у В сумму aij, если А выбрал вариант i (i=1,2,…, n), а В выбрал вариант j (j=1,2,…, m). Тогда платежная матрица для игрока А имеет вид:
A = [ a ij ] = a 21 a 22 … a 2m ……….. a n1 a n2 … a nm Если выигрыш игрока А равен проигрышу игрока В, возникает игра двух лиц с нулевой суммой. В этом случае платежную матрицу для игрока В нет необходимости рассматривать самостоятельно, так как В = – А. Лучшая (оптимальная) стратегия игрока заключается в выборе такого варианта хода (из своих возможных), при котором будет получен максимальный выигрыш при отсутствии информации о ходе противника. Определение оптимальных стратегий для игроков составляет решение игры. Игрок следует чистой стратегии в повторяющихся партиях, если в каждой партии он выбирает из всех альтернатив одну и ту же, использование комбинаций чистых стратегий называется смешанной стратегией. Для решения игры будем использовать критерий минимакса – максимина. Этот критерий предписывает игроку А выбирать такую стратегию (чистую или смешанную), которая максимизирует его минимальный выигрыш, причем минимум берется по всем стратегиям игрока В. Игрок В в свою очередь выбирает стратегию, которая минимизирует его максимальный проигрыш, где максимум берется по стратегиям игрока А. Рассмотрим применение данного критерия на примере. Игрок В
игрока А. Если игрок А выбирает первую стратегию, его А = –1 3
от поведения игрока В. При выборе игроком А второй стратегии гарантированный выигрыш будет равен miní–1, 3ý= –1, и, наконец, если он выберет третью стратегию, гарантированный выигрыш будет равен miní1,2ý= 1. Тогда игрок А, выбирая третью стратегию, максимизирует свой минимальный выигрыш. Его значение равно mахí–4, –1, 1ý=1. Выбранная игроком А стратегия называется максиминной стратегией, а соответствующее ей значение выигрыша – максиминным (нижним) значением игры. Игрок В хочет минимизировать свой проигрыш. Выбрав первую стратегию, он может проиграть не более чем mахí–2, –1, 1ý=1 независимо от выбора своего противника. При второй стратегии проигрыш составит не более mахí–4, 3, 2ý=3. Игрок В выберет тогда первую стратегию, для которой проигрыш составит miní1, 3ý=1. Эта стратегия называется минимаксной, а соответствующее ей значение проигрыша игрока В – минимаксным (верхним) значением игры. Если нижнее значение игры совпадает с верхним значением игры, то имеет место ситуация равновесия, в этом случае задача имеет решение в чистых стратегиях, в противном случае необходимо искать оптимальную смешанную стратегию. Рассмотрим еще несколько примеров матричных игр: 1. "Орлянка". Два игрока одновременно кладут на стол по монете "орлом" или "решеткой" вверх. Если "картинки" совпадут, то выигрывает первый игрок, в противном случае второй. Если в каждой отдельной партии разыгрывается некоторая единичная ставка, то матрица данной игры примет вид: A= 2. "Камень, мешок, ножницы". Это одна из древнейших тюремных игр, в которую было принято играть на пальцах. Количество выброшенных пальцев от одного до трех соответствовало выбранному предмету, при этом камень побеждал ножницы, мешок–камень и ножницы – мешок. Если игроками выбирались одинаковые предметы, то результат партии признавался ничейным. Матрица выигрышей этой игры имеет следующий вид: A= 3. Не заботясь о содержательном смысле игры, просто напишем некоторую, специальным образом построенную матрицу выигрышей A= Если в первых двух играх ситуации равновесия не существуют, так как нижнее значение игры равно -1, а верхнее значение игры равно 1, то в третьем примере maxmin{aij}=max{-2,-2,2,-2}=2 и minmax{aij}=min{4,2,3}=2, т.е. существует ситуация равновесия. Следовательно, значением этой игры будет 2, а оптимальными стратегиями для первого игрока выбор третьей строки и для второго – второго столбца матрицы игры. Отметим, что матричная игра, для которой существует ситуация равновесия, малоинтересна (и редко случается на практике), так как рациональные действия игроков в ней однозначно предопределены. Если разыгрывается несколько партий такой игры, то каждый раз исход игры будет неизменным. Если же разыгрывается несколько партий в "орлянку", то ни один из игроков не рискнет сохранять неизменной выбираемую стратегию, так как подобные действия легко "расшифровываются" противником. Возможность изменять от партии к партии свои стратегии и составляют суть любой игры, делают ее исход непредсказуемым. Однако в этом случае возникает проблема определения решения игры.
2 .7.2. Математическая модель игры. В математических обозначениях «максимин для А» выражается mахiminj aij, аналогично, «минимакс для В» есть minjmахi a ij, причем, очевидно, имеет место mахi minj aij £ minjmахi aij. В случае, когда имеет место равенство, т.е. mахi minj aij = minjmахi aij = а i0j0, соответствующие чистые стратегии (i0 для игрока А и j0 для В) будут оптимальными, а про игру говорят, что она имеет седловую точку. Тогда а i0j0 является значением игры. Легко видеть, что игра имеет седловую точку тогда и только тогда, когда в платежной матрице имеется элемент а i0j0, наименьший для всех элементов своей строки i0 и наибольший для всех элементов своего столбца j0. При отсутствии седловой точки невозможно получить оптимальное решение, пользуясь чистыми стратегиями. В этом случае для получения решения игры будем пользоваться смешанными стратегиями, которые заключаются в применении чистых стратегий с некоторыми частотами (вероятностями). Пусть р 1, р 2,.., р n и q 1, q 2,.., q m – наборы вероятностей, с которыми игроки А и В соответственно выбирают свои чистые стратегии. Естественно
Если игрок А выбирает свои чистые стратегии с вероятностями рi, то его ожидаемый выигрыш должен составить a 11 р 1+ a 21 р 2+…+ a n1 рn, при ответном выборе игроком В своей первой чистой стратегии, a 12 р 1+ a 22 р 2+…+ a n2 рn, при ответном выборе игроком В своей второй чистой стратегии, и т.д. a 1m р 1+ a 2m р 2+…+ a nm рn при выборе игроком В m-й чистой стратегии. С другой стороны, если игрок В выбирает свои чистые стратегии с вероятностями qj, то его ожидаемый проигрыш должен составить a 11 q 1+ a 12 q 2+…+ a 1m q m, если игрок A выберет свою первую чистую стратегию, и т.д. a n1 q 1+ a n2 q 2+…+ a nm qm, при выборе игроком A n-й чистой стратегии. Если игрок А выбрал стратегию (р 1, р 2,.., рn) и при этом игрок В выбрал (q 1, q 2,.., q m), то ожидаемый выигрыш игрока А (он же проигрыш игрока В) составит g= Тогда игрок А при выборе р i стремится максимизировать свой наименьший ожидаемый выигрыш по столбцам, тогда как игрок В выбирает q j с целью минимизировать наибольший ожидаемый проигрыш по строкам. Справедлива теорема фон.Неймана, которую мы примем без доказательств, утверждающая, что для любой конечной игры существуют оптимальные стратегии игроков А (р 1*, р 2*,.., рn *) и В (q 1*, q 2*,.., qm *), при этом максимум наименьшего ожидаемого выигрыша игрока А совпадает с минимумом наибольшего ожидаемого проигрыша игрока В (обозначим это значение игры через g). Таким образом, математическую модель конечной игры для игрока А можно представить в следующем виде: Найти такие рi ≥0, для которых выполняются соотношения
a 11 р 1+ a 21 р 2+…+ a n1 рn ≥ g, a 12 р 1+ a 22 р 2+…+ a n2 рn ≥g, (2.7.1) ……………………. …… a 1m р 1+ a 2m р 2+…+ a nm рn ≥ g, и функция Z=g принимает максимальное значение. Упростим полученную задачу, разделив все ограничения (2.7.1) на значение игры g > 0 и положив х i = рi /g для всех i. (Проведение аналогичных рассуждений для случая g ≤ 0 предоставляется читателю). В силу того, что max g =min 1/g = min(р 1/g+ р 2/g+…+ рn /g) = min(x 1+ x 2+…+ x n) задача принимает вид минимизировать Z= x 1+ x 2+…+ x n при ограничениях
a 12 x 1+ a 22 x 2+…+ a n2 x n ≥ 1, (2.7.2) ……………………. …… a 1m x 1+ a 2m x 2+…+ a nm x n≥ 1, x 1, x 2,…, x n ≥ 0. Мы получили задачу линейного программирования (см. 2.2). Обратите внимание: строка ограничения формируется из столбца платежной матрицы! Решая ее (например, симплекс–методом), находим оптимальное решение x 1*, x 2*,…, x n*, откуда, разделив на Z*= x 1*+ x 2*+…+ x n*, получаем оптимальную стратегию для игрока А (р 1*, р 2*,.., рn *), которая заключается в применении i-й чистой стратегии с частотой рi *= хi */ Z*. Двойственная ЗЛП – максимизировать F = y 1+ y 2+ … + y m→max;
a 11 y 1+ a 12 y 2+ …+ a 1m y m ≤1; a 21 y 1+ a 22 y 2+ …+ a 2m y m ≤1; (7.2.3) ………………………….. a n1 y 1+ a n2 y 2+ …+ an m y m ≤1; y 1≥0; y 2≥0; … y m ≥0. Здесь строка ограничения формируется из строки платежной матрицы. Решая данную ЗЛП, находим оптимальное решение у 1*, у 2*,…, у m*, откуда, разделив на F *= y 1*+ y 2*+…+ y m*, получаем оптимальную стратегию для игрока B (q 1*, q 2*,.., qm *), которая заключается в применении j-й чистой стратегии с частотой qj * = yj */ F *. Затем находим цену игры g =1/ Z* =1 /F*. Правила упрощения платежной матрицы: Если к каждому элементу платежной матрицы прибавить одно и то же число, то решение (р 1*, р 2*,.., рm *) не изменится, а цена игры изменится ровно на добавленную величину. Если каждый элемент платежной матрицы умножить на одно и то же число (не 0), то решение (р 1*, р 2*,.., рm *) не изменится, а цена игры изменится ровно во столько же раз. Если какая-либо строка платежной матрицы доминирует над другой строкой (или линейной комбинацией строк), то доминируемые строки не войдут в оптимальную смешанную стратегию и их можно удалить. Из двух стратегий та "лучше" (доминирует), которая гарантирует больший выигрыш независимо от действий противника (исходов). Ясно, что доминирующая над всеми строка, если она существует, будет являться чистой оптимальной стратеией первого игрока. Однако, в общем случае, строки, доминирующей над всеми другими строками, может и не существовать. Проиллюстрируем использование рассмотренных методов при описании и решении некоторых состязательных задач. Пример 2.7.1. Рассмотрим тотализатор на ипподроме. Пусть выплаты в случае победы одной из трех лошадей относятся к ставке как 1:1, 3:1 и 4:1. Тогда платежная матрица игрока на скачках примет вид:
А=–1 3 –1 оптимальные стратегии не изменятся, а значение игры –1 –1 4 увеличится на К. Для упрощения матрицы добавим К=1, тогда получим:
А= 0 4 0 минимизировать Z= x 1+ x 2+ x 3 0 0 5 при ограничениях
0 x 1+ 4 x 2+0 x 3 ≥ 1, 0 x 1+ 0 x 2+5 x 3≥ 1, x 1, x 2, x 3 ≥ 0. Легко заметить, что решение этой задачи: x 1*=1/2, x 2*=1/4, x 3* =1/5. Значение упрощенной игры 1/Z*=1/(x 1*+ x 2*+ x 3*)=20/19, откуда (при К=1) значение исходной игры равно 20/19 – 1 = 1/19, р 1*= х 1*/Z*=10/19, р 2*= х 2*/Z*=5/19, р 3*= х 3*/Z*=4/19. Таким образом, оптимальная стратегия игрока на скачках в данном примере заключается в смешанной стратегии делать ставки на всех трех лошадей в пропорции 10:5:4, при этом выигрыш игрока (игра имеет положительное значение!) будет равным 1/19 суммы его ставок, независимо от результата гонок. (Если цена игры отрицательна, то не следует в нее играть, так как даже при оптимальной стратегии гарантирован проигрыш, правда, минимальный). Пример 2.7.2. Предлагается три варианта инвестиций в сельское хозяйство и прогноз получения доходов за год (дивиденды и повышение стоимости капитала) при различных перспективах на урожай.
Доходы в платежной матрице приведены в процентах от вложенного капитала. Как распорядиться капиталом, чтобы получить наибольший доход? Искомые переменные р 1, р 2, р 3 определяют пропорции вложений. Заметим, что элементы первой строки платежной матрицы меньше средних арифметических соответствующих элементов второй и третьей строк, и она может быть удалена (первый вариант инвестиций заведомо неэффективен по сравнению с комбинацией второго и третьего вариантов – вкладывать деньги поровну во второй и третий проект). Получаем задачу линейного программирования минимизировать Z= x 2+ x 3 при ограничениях
100 x 2+50 x 3 ≥ 1, 250 x 2 – 50 x 3≥ 1, x 1=0, x 2, x 3 ≥ 0. Решая данную задачу стандартными средствами (см.2.2) получим следующее решение x 1*=0, x 2*=1/150, x 3* =1/150. Значение игры 1/Z*=1/(x 1*+ x 2*+ x 3*)=150/2=75, откуда р 1*=0, р 2*= х 2*/Z*=75/150=1/2, р 3*= х 3*/Z*=75/150=1/2. Таким образом, оптимальной стратегией является вложение капитала равными долями во второй и третий варианты, при этом гарантированный доход составит 75%.
|




 a 11 a 12 … a 1m
a 11 a 12 … a 1m

 .
.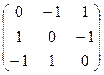 .
.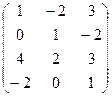 .
. =1, рi, qj ≥0 для всех i и j.
=1, рi, qj ≥0 для всех i и j. .
. р 1+ р 2+…+ рn =1,
р 1+ р 2+…+ рn =1, a 11 x 1+ a 21 x 2+…+ a n1 x n ≥ 1,
a 11 x 1+ a 21 x 2+…+ a n1 x n ≥ 1, при ограничениях
при ограничениях
 1 –1 –1 Если прибавить к каждому элементу матрицы число К, то
1 –1 –1 Если прибавить к каждому элементу матрицы число К, то
 2 0 0 В соответствие с (2.7.2) задача принимает вид:
2 0 0 В соответствие с (2.7.2) задача принимает вид: 2 x 1+ 0 x 2+0 x 3 ≥ 1,
2 x 1+ 0 x 2+0 x 3 ≥ 1, 0 x 2 + 150 x 3 ≥ 1,
0 x 2 + 150 x 3 ≥ 1,


