Теплообмен при вынужденном течении в трубах
При входе потока в трубу на ее стенках образуется пограничный слой. На некотором расстоянии lТ от входного сечения называемым начальным участком гидродинамической стабилизации, пограничный слой занимает все сечение трубы и безразмерный профиль скорости
Длина участка гидродинамической стабилизации аппроксимируется формулой Скорость в ядре потока U0 увеличивается в соответствии с зависимостью
Интенсивность теплообмена на начальном участке аппроксимируется зависимостью, полученной при исследовании теплообмена при обтекании плоской пластины
где Длина участка термической стабилизации находится по формуле
При числах Re < ReКР в трубах происходят ламинарное течение, описываемое уравнениями Навье – Стокса в цилиндрической системе координат. Пренебрегая для участка стабилизированного течения радиальной Ur и окружной Uφ cоставляющими скорости получим для Ux=U
На участке стабилизации Интегрируя (8.68) находим
Константы при r = 0,
Профиль скорости при ламинарном течении жидкости в трубе имеет параболический вид
где х = х1 и х = х2.. При этом средняя по сечению скорость потока
Выражая из (8.72)
Потери давления в трубах выражаются по формуле
Тогда из (8.60) получаем
где Применим уравнение энергии для расчета теплообмена в цилиндрической трубе при гидравлически стабилизированном ламинарном течении. Процесс считаем установившимся, жидкость несжимаемая, теплофизические свойства считаем постоянными. Пренебрегаем теплом трения и тепловым потоком вдоль трубы. Принимаем в соответствие с (8.73)
Вводя переменные
Задачу решаем при постоянстве температуры стенки трубы (Тст= соnst) Граничные условия имеют вид
Решение дифференциального уравнения (8.75) ищем методом разделения нерешенных, полагая
Подставим (8.76) в (8.75) получим
Разделяя переменные получим
Уравнение (8.78) имеет решение
Где Решение уравнения (8.75) при условии постоянства удельного теплового протока по длине трубы qСТ= соnst приводит к значению Nud≈4,36. При ламинарном течении жидкости в вертикальной трубе при постоянной тепловой нагрузке и совместном проявлении вынужденной и естественной конвекции Б.С. Петуховым получено
Где Nu0 определяется при постоянных свойствах,
Уравнение (8.81) применимо при
При ламинарном течении в горизонтальной трубе и совместном действии вынужденной и естественной конвекции при
где Формула для определения среднего по длине коэффициента теплоотдачи при вынужденном ламинарном движении жидкости в трубе, учитывающая влияние свободной конвекции и направление теплового потока, может быть представлено в виде
где нижний индекс f, это физические параметры определяются при температуре жидкости, СТ – при температуре стенки. При Re < ReКР в условиях турбулентного течения коэффициент трения ξ зависит от двух переменных числа Теплоотдачу для гладких труб в диапазоне чисел
где в качестве определяющего размера принимается эквивалентный диаметр
Для воздуха формула упрощается
|

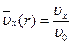 стабилизируется на начальном участке термической стабилизации lТ в несжимаемой жидкости при ТСТ = соnst стабилизируется безразмерный профиль температуры
стабилизируется на начальном участке термической стабилизации lТ в несжимаемой жидкости при ТСТ = соnst стабилизируется безразмерный профиль температуры
 . На этом участке развивается пограничный слой, характеризующийся толщиной вытеснения δ*.
. На этом участке развивается пограничный слой, характеризующийся толщиной вытеснения δ*. . Число
. Число  Коэффициент трения
Коэффициент трения 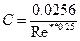 .
. (8.68)
(8.68)

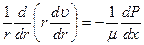 , (8.69)
, (8.69)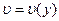 , а
, а 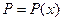 , следовательно
, следовательно 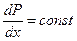
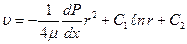 (8.70)
(8.70)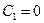 и
и  находятся из условий
находятся из условий 

 = 0 при r = r0, где r0 - радиус трубы.
= 0 при r = r0, где r0 - радиус трубы.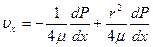
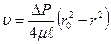 (8.71)
(8.71) - изменение давления на участке длиной l между сечениями
- изменение давления на участке длиной l между сечениями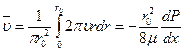 (8.72)
(8.72)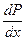 и подставляя в (8.71) получим профиль скорости Блазиуса
и подставляя в (8.71) получим профиль скорости Блазиуса (8.73)
(8.73)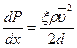
 , (8.74)
, (8.74)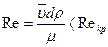
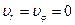
 . Тогда
. Тогда 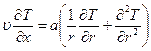 .
.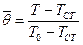 ,
, 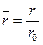 и
и  , получим
, получим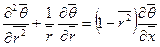 (8.75)
(8.75)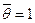 при
при 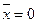 ,
, 
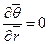 при
при 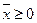 ,
, 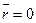
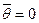 при
при 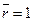
 (8.76)
(8.76)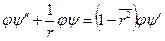 (8.77)
(8.77)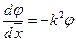 и (8.78)
и (8.78) (8.79)
(8.79) , а (8.79) может решаться стандартным численным методом. Полученное решение при
, а (8.79) может решаться стандартным численным методом. Полученное решение при  аппроксимируется критериальным уравнением
аппроксимируется критериальным уравнением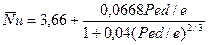 , (8.80)
, (8.80) ,
, 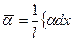 - средний на длине трубы l коэффициент теплоотдачи
- средний на длине трубы l коэффициент теплоотдачи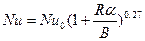 (8.81)
(8.81)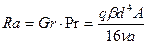 - число Рэлея,
- число Рэлея, 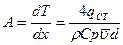 ,
,  при х < 0,07; В = 60 при х ≥ 0,07;
при х < 0,07; В = 60 при х ≥ 0,07;  ,
, 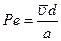 ,
,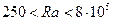 ;
;  ;
; 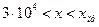 ;
; 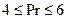 .
.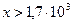 получено
получено (8.82)
(8.82)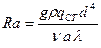 .
. (8.83)
(8.83)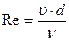 и относительной шероховатости и приводится в справочной литературе.
и относительной шероховатости и приводится в справочной литературе. для труб круглого, квадратного, прямоугольного, треугольного, кольцевого
для труб круглого, квадратного, прямоугольного, треугольного, кольцевого 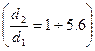 , щелевого
, щелевого 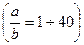
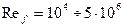 и числах
и числах 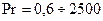 можно определять по формуле М.А. Михеева
можно определять по формуле М.А. Михеева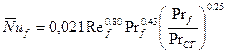 (8.84)
(8.84) , П - периметр.
, П - периметр. (8.85)
(8.85)


