Интегральные модели тепломассопереноса в турбулентном пограничном слое
Интегральные уравнения движения, энергии и диффузии выводятся из уравнений (8.38), (8.41) и (8.46) в таком же порядке, как и интегральные уравнения ламинарного слоя (п. 7.3). При этом коэффициенты - уравнение импульсов
- уравнение энергии
- уравнение диффузии
Уравнения (8.53), (8.54), (8.55) по виду совпадают с аналогичными уравнениями для ламинарного пограничного слоя. Однако зависимости для параметров Коэффициент трения в стандартных условиях на пластине при Pr = 1, Sc = 1, обычно представляют в степенном виде
где В = 0,0252, m = 0,25 при Re** < 104. Числа Стантона и диффузионного числа Стантона при
Влияние теплофизических свойств сред учитывается отличием чисел Pr и Sc от 1:
Числа
Решением (8.59) является
Влияние сжимаемости газа и неизотермичности учитывается введением относительных законов трения, тепло- и массообмена
где Относительный закон теплообмена с достаточной для практики точностью может быть определен по предельным законам Кутателадзе – Леонтьева
где
Подвод газа через поверхность (вдув) существенно снижает интенсивность теплообмена. При параметрах вдува
При параметрах вдува
где В случае постоянной плотности
Касательное напряжение трения, удельный тепловой поток и удельный диффузионный потоки при вынужденном турбулентном обтекании поверхности определяется с учетом относительных параметров
Соотношения (8.51) – (8.53), (8.63) – (8.67) составляют основу многих инженерных методик расчета трения и тепломассообмена при вынужденном обтекании поверхностей.
|

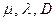 заменяются эффективными коэффициентами
заменяются эффективными коэффициентами 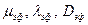 . Для турбулентного пограничного слоя получают
. Для турбулентного пограничного слоя получают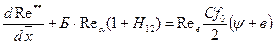 (8.53)
(8.53) (8.54)
(8.54) (8.55)
(8.55)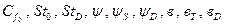 для турбулентных и ламинарных режимов течения существенно размягчаются. Основной метод, который используется для определения этих параметров – накопление и обобщение экспериментальных данных.
для турбулентных и ламинарных режимов течения существенно размягчаются. Основной метод, который используется для определения этих параметров – накопление и обобщение экспериментальных данных.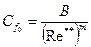 (8.56)
(8.56) записывают в виде аналогичном (8.56)
записывают в виде аналогичном (8.56)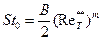 ;
;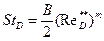 (8.57)
(8.57)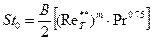
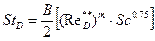 (8.58)
(8.58)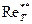 и
и  для стандартных условий обтекания плоской пластины находятся, с учетом (8.58), из уравнений энергии и диффузии при граничных условиях х = 0,
для стандартных условий обтекания плоской пластины находятся, с учетом (8.58), из уравнений энергии и диффузии при граничных условиях х = 0, 
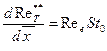
 (8.59)
(8.59) (8.60)
(8.60)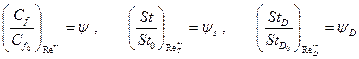 (8.61)
(8.61)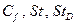 - коэффициенты трения, число Стантона с учетом сжимаемости и изотермичности, при тех числах
- коэффициенты трения, число Стантона с учетом сжимаемости и изотермичности, при тех числах 
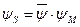 , (8.62)
, (8.62)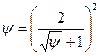 ,
, 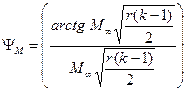 ,
, , коэффициент восстановления температуры на стенке r ≈ 0,9 для турбулентного пограничного слоя, К – показатель адиабаты газа.
, коэффициент восстановления температуры на стенке r ≈ 0,9 для турбулентного пограничного слоя, К – показатель адиабаты газа.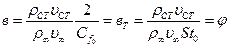 , называемых критическими параметрами вдува относительные параметельные параметры трения и теплообмена
, называемых критическими параметрами вдува относительные параметельные параметры трения и теплообмена 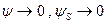 .
. относительные законы трения и теплообмена описываются предельными законами трения и теплообмена Кутателадзе – Леонтьева.
относительные законы трения и теплообмена описываются предельными законами трения и теплообмена Кутателадзе – Леонтьева.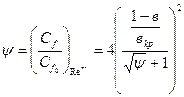 , (8.63)
, (8.63)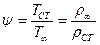
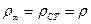 при
при 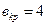 уравнение (8.63) имеет вид
уравнение (8.63) имеет вид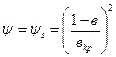 (8.64)
(8.64)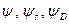 :
: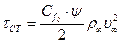 (8.65)
(8.65) (8.66)
(8.66)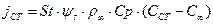 (8.67)
(8.67)


