Характерные толщины пограничных слоев. Интегральное соотношение импульсов.
Дифференциальные уравнения пограничного слоя, решаемые численными методами, требуют задания граничных условий трения и тепломассобмена. Для этого необходимы обобщение опытных данных. Существенные практические результаты достигнуты путем применения уравнений импульсов, энергии и диффузии в интегральной форме. Важными для расчетов характеристиками являются толщина вытеснения δ*, толщина потери импульса δ**, толщина потери энергии (энтальпии) δт** и толщина потери вещества δD**. Толщину вытеснения δ* определяют как отрезок по нормали к стенке, через который массовый расход идеальной жидкости был бы равен потере расхода в сечении пограничного слоя из-за диссипативных потерь вследствие трения и вихреобразования
откуда
Толщина потери импульса δ** - это отрезок по нормали к стенке, через который при течении идеальной жидкости проходило бы секундное количество движения, равное потере количества движения, равное потери количества движения в сечении пограничного слоя, вследствие трения и вихреобразования:
откуда
Толщина потери энтальпии - это такое расстояние от стенки по нормали, через которое при течении идеальной жидкости проходит секундное количество разности полной энтальпии
откуда
Толщина потери i-ого вещества δD** - расстояние от стенки по нормали, через которое при течении идеальной жидкости проходило бы секундное количество i-ого вещества при массообмене
откуда
Интегральное соотношение потери количества движения получается интегрированием уравнения движения в проекции на ось х (7.6). Интегрирование ведется по у от у = 0 до у = δ. Используется также уравнение неразрывности (7.5). После преобразований получают
где При обтекании поверхности несжимаемой жидкостью или газом при числе Маха М < 1 и отсутствие массообмена через поверхность уравнения (7.61) имеет вид
Соотношение(7.61) замыкается модельным уравнением, найденным при экспериментах, обобщенных опытных данных
где Рi –параметры и функции, найденные опытным путем, коэффициент трения Сf зависит от Для системы двух дифференциальных уравнений (7.63), (7.64) ставятся два начальных условия х = 0, δ** = δо**, Н12 = Н120 (7.65) Решение системы уравнений (7.62), (7.64) с граничными условиями (7.65) относится к задачам Коши, которые решаются стандартными численными методами (метод Рунге – Кутта и др.).
|

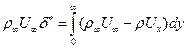 (7.54)
(7.54)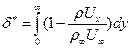 (7.55)
(7.55)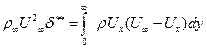 (7.56)
(7.56)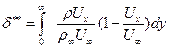 (7.57)
(7.57)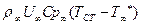 , равное разности энтальпии в реальном потоке
, равное разности энтальпии в реальном потоке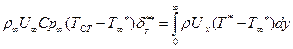 , (7.58)
, (7.58)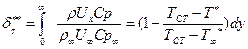 (7.59)
(7.59)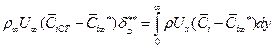 (7.60)
(7.60)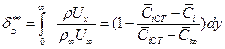 (7.61)
(7.61)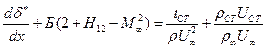 (7.62)
(7.62)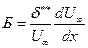 - параметр, характеризующий характер изменения скорости
- параметр, характеризующий характер изменения скорости 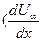 > 0 – конфузорное течение,
> 0 – конфузорное течение, 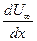 < 0 – диффузорное течение) при обтекании поверхности. Предистория течения в пограничном слое отражается на толщине потери импульсов в сечении δ** и форм параметра
< 0 – диффузорное течение) при обтекании поверхности. Предистория течения в пограничном слое отражается на толщине потери импульсов в сечении δ** и форм параметра 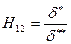 . Число Маха равно
. Число Маха равно 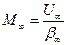 , где
, где 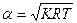 - скорость звука; Ucт – проекция скорости на (п. 7) ось х при подводе или отводе массы через стенку.
- скорость звука; Ucт – проекция скорости на (п. 7) ось х при подводе или отводе массы через стенку.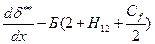 (7.63)
(7.63)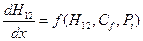 , (7.64)
, (7.64)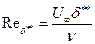 и Н12
и Н12


