Уравнение Навье-Стокса.
Рассмотрим уравнения движения в напряжениях () применительно к линейно-вязким средам. Жидкость полагаем несжимаемой
Преобразуем первое из уравнений (4.14)
(4.15) Для несжимаемой жидкости
Аналогично, из 2-го и 3-го уравнений (4.14) получим уравнения движения в проекции на оси
Уравнения движения в проекции на оси
где Для сжимаемой среды тензор напряжений (при
или в компонентной форме
Преобразуем первое из уравнений (4.14), с учетом (4.17)
(4.18) Тогда из (4.14)
Аналогично из 2-го и 3-го уравнений (4.14):
В векторной форме уравнение Навье-Стокса для вязкой сжимаемой среды приобретает вид
|

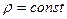 с постоянным коэффициентом вязкости
с постоянным коэффициентом вязкости  . Введем декартову систему координат
. Введем декартову систему координат 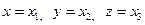 . Уравнения движения запишем в проекциях на оси
. Уравнения движения запишем в проекциях на оси 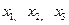 :
: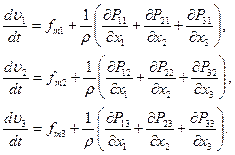 (4.14)
(4.14)
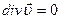 и, следовательно, первое из уравнений (4.14) можно записать в виде
и, следовательно, первое из уравнений (4.14) можно записать в виде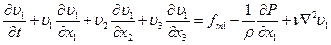
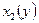 и
и 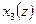 :
: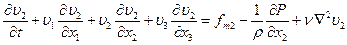 ,
,
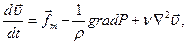 (4.16)
(4.16) - лапласиан
- лапласиан 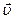 соответствует вектору с проекциями
соответствует вектору с проекциями 
 ) имеет вид (4.13)
) имеет вид (4.13)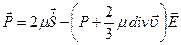
 (4.17)
(4.17)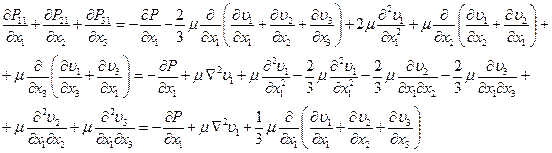
 ;
;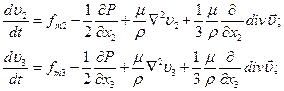 (4.19)
(4.19) (4.20)
(4.20)


