Уравнение движения в дифференциальной форме (в напряжениях)
Преобразуем интегралы по поверхности S в (13.14) и (33.16) в интегралы по объему V, воспользовавшись формулами Гаусса-Остроградского:
Тогда для однофазной среды в декартовой системе координат
Ввиду произвольности объема V, подынтегральная функция в (7) равна нулю. Тогда, с учетом уравнения неразрывности, получим уравнение движения в дифференциальной форме:
Для каждой i -ой фазы
где
|

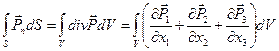 (5)
(5)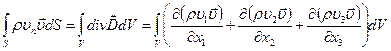 (6)
(6)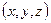 :
: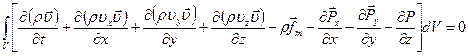 (7)
(7)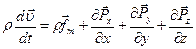 (8)
(8)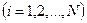 из уравнения (2) получим, проводя преобразование аналогичные соотношения (3) – (8), с учетом уравнения неразрывности i -ой фазы:
из уравнения (2) получим, проводя преобразование аналогичные соотношения (3) – (8), с учетом уравнения неразрывности i -ой фазы: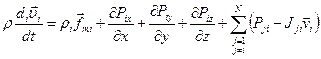 (9)
(9)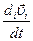 – производная, связанная с движением i -ой фазы.
– производная, связанная с движением i -ой фазы.


