Квазиодномерное течение несжимаемой жидкости.
Уравнение расхода и уравнение баланса кинетической энергии, отнесённой к 1 кг рабочего тела, запишется в виде:
где
- удельная работа вязких сил, учитывающая потери энергии на трение жидкости о стенки канала - Для длинных каналов, в которых преобладают потери трения Уравнение (6.2) называется уравнением Бернулли. При течении невязкой жидкости ℓтр=0. Рассмотрим течение вязкой несжимаемой жидкости (ρ=const) в канале с заданным поперечным сечением (s=s(x)) и с известным высотным положением (z=z(x)).
Уравнение Д. Бернулли приобретает вид:
Система уравнений (6.1) и (6.2) с замыкающим соотношением (6.3) при заданном высотном положении канала Z=Z(x), заданном сечении канала S=S(x), известном объёмном расходе Q= Для реальной вязкой жидкости при ℓтехн=0,
Уравнение (6.4) обобщает уравнение Бернулли (6.3) на случай течения вязкой жидкости с потерями энергии.
В частности для выходного сечения можно записать:
Соотношения (6.5) и (6.6) могут быть названы основными соотношениями гидравлики. Они широко используются при расчете течений жидкости в трубах ( Важным случаем использования основных соотношений гидравлики (6.6) является решение задачи об определении объёмного расхода Q на участке трубопровода (x1,x2) если известен (например измерен) перепад давления в сечениях 1 и 2:∆P=P1-P2. Тогда из (6.7) получаем формулу округления объёмного расхода через канал:
Рассмотрим 2 частных случая соотношения (6.8), широко применяемых на практике: 1. Канал, на котором установлена диафрагма или иное местное сопротивление и
2. Участок трубопровода с постоянным диаметром без местных сопротивлений (S1=S2,
где
|

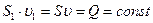 (6.1)
(6.1)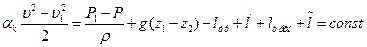 (6.2)
(6.2)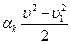 - изменение удельной кинетической энергии,
- изменение удельной кинетической энергии, 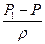 - удельная работа сил давления,
- удельная работа сил давления, 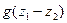 - удельная работа внешних массовых сил – сил трения, ℓ’ – работа, связанная с обменом импульсом через боковые стенки, ℓтехн – удельная работа подведённая в насос,
- удельная работа внешних массовых сил – сил трения, ℓ’ – работа, связанная с обменом импульсом через боковые стенки, ℓтехн – удельная работа подведённая в насос, 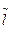 - работа сил инерции.
- работа сил инерции.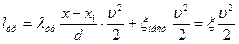 (6.3)
(6.3)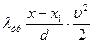 и потери энергии при вихреобразовании на местных сопротивлениях (вентили, диафрагмы, резкое изменение сечения канала и т.п.) -
и потери энергии при вихреобразовании на местных сопротивлениях (вентили, диафрагмы, резкое изменение сечения канала и т.п.) - 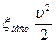 , где
, где 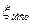 - известные из справочной литературы коэффициенты потерь на местных сопротивлениях,
- известные из справочной литературы коэффициенты потерь на местных сопротивлениях, 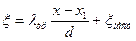 - эквивалентный коэффициент сопротивления, учитывающий потери трения и местные потери.
- эквивалентный коэффициент сопротивления, учитывающий потери трения и местные потери.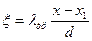 , для коротких каналов, где преобладают потери на местных сопротивлениях, например на измерительных диафрагмах,
, для коротких каналов, где преобладают потери на местных сопротивлениях, например на измерительных диафрагмах, 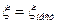 .
.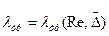 - коэффициент трения – известная функция от числа Рейнольдса (
- коэффициент трения – известная функция от числа Рейнольдса (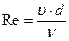 ) и относительной шероховатости (
) и относительной шероховатости (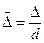 ), d – эквивалентный диаметр канала,
), d – эквивалентный диаметр канала, 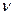 - коэффициент кинематической вязкости, Q=G/ p, м3/с – объёмный расход жидкости в канале. Для идеальной невязкой жидкости ℓтр=0, αk=1,0.
- коэффициент кинематической вязкости, Q=G/ p, м3/с – объёмный расход жидкости в канале. Для идеальной невязкой жидкости ℓтр=0, αk=1,0.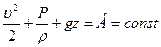 (6.4)
(6.4)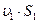 и известном давлении во входном сечении определяют изменение скорости
и известном давлении во входном сечении определяют изменение скорости 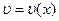 и давления
и давления 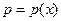 по длине канала.
по длине канала.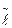 =0 и ℓ=0, уравнение (6.2), с допущением
=0 и ℓ=0, уравнение (6.2), с допущением 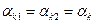 , записывается в виде:
, записывается в виде: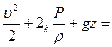
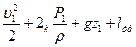 (6.5)
(6.5)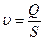 ,
,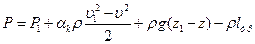 (6.6)
(6.6)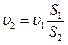 ,
,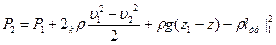 (6.7)
(6.7)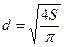 ) и каналах переменного сечения (S=S(x)).
) и каналах переменного сечения (S=S(x)).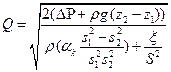 (6.8)
(6.8)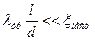 (z1=z2,S1=S2,
(z1=z2,S1=S2, 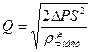 (6.9)
(6.9) ):
):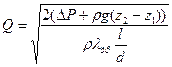 , (6.10)
, (6.10)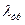 вычисляется итерациями с учётом
вычисляется итерациями с учётом 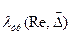 , где
, где 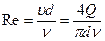 , т.к
, т.к 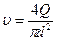 .
.


