Уравнение баланса кинетической энергии
Известная из курса теоретической механики теорема об изменении кинетической энергии системы материальных точек устанавливает, что производная по времени от кинетической энергии системы материальных точек равна сумме мощностей внешних Для сплошной среды эта теорема обобщается в следующем виде: индивидуальная производная по времени от кинетической энергии движущегося объема
где первый интеграл в правой части представляет собой мощность внешних объемных сил, второй интеграл – мощность внешних поверхностных сил, сумма этих интегралов равна Для получения дифференциальной формы записи уравнение (103.23) преобразуется следующим образом: используя тождество
и формулу Остроградского-Гаусса из (103.23) получаем:
Ввиду произвольности объема
Умножим скалярно уравнение движения в напряжениях (83.21) на вектор скорости
Почленно вычтем (123.25) из (113.24) и получим:
Воспользуемся тождествами
где Тогда из (133.26) получим:
Разложим
и антисимметричную часть
При этом Тензор напряжений
Уравнение баланса кинетической энергии (113.24) с учетом (153.28) запишется в виде:
|

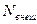 и внутренних
и внутренних  сил.
сил.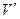 среды равна сумме мощностей внешних и внутренних сил, действующих на выделенную массу.
среды равна сумме мощностей внешних и внутренних сил, действующих на выделенную массу. (103.23)
(103.23)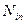 – плотность распределения мощности внутренних сил). Уравнение (103.23) является уравнением баланса кинетической энергии в интегральной форме.
– плотность распределения мощности внутренних сил). Уравнение (103.23) является уравнением баланса кинетической энергии в интегральной форме.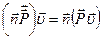
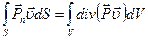 ,
,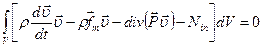
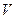 приравниваем к нулю подынтегральную функцию. Тогда получим уравнение баланса кинетической энергии в дифференциальной форме.
приравниваем к нулю подынтегральную функцию. Тогда получим уравнение баланса кинетической энергии в дифференциальной форме.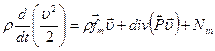 (113.24)
(113.24)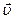 :
: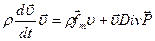 (123.25)
(123.25)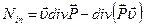 (133.26)
(133.26)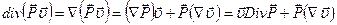
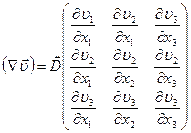 – диада (тензор) вектора скорости с компонентами
– диада (тензор) вектора скорости с компонентами 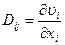 , (
, (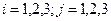 ).
).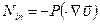 (143.27)
(143.27)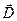 на симметричную часть
на симметричную часть 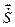 – тензор скоростей деформаций с компонентами
– тензор скоростей деформаций с компонентами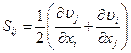
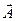 – тензор ротации поля скорости с компонентами
– тензор ротации поля скорости с компонентами
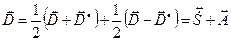
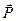 – симметричный тензор. Произведение симметричного тензора
– симметричный тензор. Произведение симметричного тензора 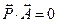 и из (143.27) получаем выражения плотности распределения внутренних сил
и из (143.27) получаем выражения плотности распределения внутренних сил 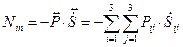 (153.28)
(153.28)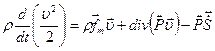 (163.29)
(163.29)


