Удельная полная энергия 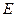 равна сумме удельных внутренних и кинетической энергии
равна сумме удельных внутренних и кинетической энергии 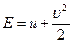 . Закон сохранения полной энергии является обобщением первого начала термодинамики для движения сплошных сред и формулируется следующим образом: индивидуальная производная по времени от полной энергии массы среды, содержащейся в движущемся объеме
. Закон сохранения полной энергии является обобщением первого начала термодинамики для движения сплошных сред и формулируется следующим образом: индивидуальная производная по времени от полной энергии массы среды, содержащейся в движущемся объеме 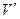 равна сумме мощностей, приложенных к выделенному объему и его поверхности внешних массовых и поверхностных сил и отнесенного к единице времени количества тепловой и немеханических видов энергии, подведенной извне к данной массе. Этот закон выражается в следующей интегральной форме:
равна сумме мощностей, приложенных к выделенному объему и его поверхности внешних массовых и поверхностных сил и отнесенного к единице времени количества тепловой и немеханических видов энергии, подведенной извне к данной массе. Этот закон выражается в следующей интегральной форме:
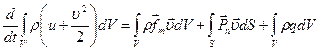 (3.30)
(3.30)
где 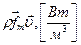 – удельная мощность объемных сил;
– удельная мощность объемных сил;  – удельная мощность поверхностных сил;
– удельная мощность поверхностных сил; 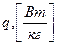 – удельная, отнесенная к единице массы тепловая и иные немеханические виды мощности подведенные извне.
– удельная, отнесенная к единице массы тепловая и иные немеханические виды мощности подведенные извне.
Третий интеграл в правой части уравнения (3.30) выражается суммой:
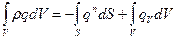 (3.31)
(3.31)
где 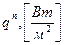 – удельная, отнесенная к единице площади поверхности, тепловая мощность;
– удельная, отнесенная к единице площади поверхности, тепловая мощность; 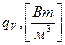 – удельная мощность объемных немеханических источников энергии.
– удельная мощность объемных немеханических источников энергии.
Для многих случаев течения сплошных сред можно полагать 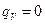 и уравнение (3.30) записывают в виде:
и уравнение (3.30) записывают в виде:
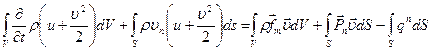 (3.32)
(3.32)
Интегральная форма записи уравнения баланса энергии может быть преобразована к алгебраической. Для этого область течения разбивается на конечное число фиксированных в пространстве малых но конечных контрольных объемов (КО) – 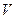 . Полагают, что в пределах КО параметры изменяются линейно или экспоненциально по пространственным координатам и времени. Производные заменяются отношением приращения функций к приращениям аргументов, например:
. Полагают, что в пределах КО параметры изменяются линейно или экспоненциально по пространственным координатам и времени. Производные заменяются отношением приращения функций к приращениям аргументов, например:
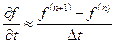 ,
, 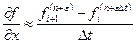 , (3.33)
, (3.33)
где индексы 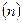 ,
, 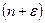 ,
, 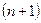 соответствуют моментам времени
соответствуют моментам времени 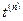 ,
,  ,
, 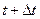 соответственно,
соответственно, 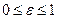 , значениям соответствуют неявные схемы,
, значениям соответствуют неявные схемы,  – явная схема. Интегралы заменяются произведениями средних значений по площади
– явная схема. Интегралы заменяются произведениями средних значений по площади 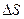 или объему
или объему 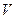 на эти площади и объемы:
на эти площади и объемы:
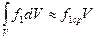 ,
, 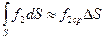 . (3.34)
. (3.34)
Тогда уравнения баланса полной энергии (3.32) для каждого контрольного объема 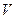 записывается в виде:
записывается в виде:
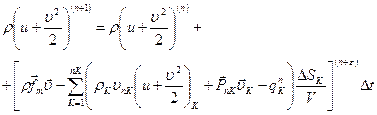 , (3.35)
, (3.35)
где 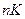 – число граней контрольного объема,
– число граней контрольного объема, 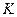 – номер грани.
– номер грани.
Таким образом (3.34) представляет собой уравнение баланса полной энергии в алгебраической форме. Это уравнение может быть использовано при построении ряда вычислительных алгоритмов для расчета течений.
Для получения дифференциального уравнения баланса полной энергии преобразуем левую часть (3.23), используя закон сохранения массы:

Поверхностный интеграл в правой части (3.23) преобразуем в объемный по формуле Остроградкого-Гаусса.
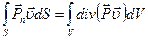
Тогда из (3.23) получим:
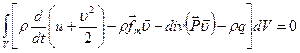 . (3.36)
. (3.36)
Ввиду произвольности 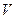 можно приравнять подынтегральную функцию в (3.36)
можно приравнять подынтегральную функцию в (3.36)
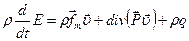 (3.37)
(3.37)
Уравнение (3.37) представляет собой уравнение баланса полной энергии 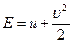 в дифференциальной форме.
в дифференциальной форме.
Уравнение баланса полной энергии  (где N – число фаз в интегральной форме) для
(где N – число фаз в интегральной форме) для 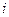 -ой фазы аналогично (3.32), однако включает в себя слагаемое
-ой фазы аналогично (3.32), однако включает в себя слагаемое 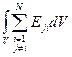 , которое характеризуется интенсивностью обмена энергией между
, которое характеризуется интенсивностью обмена энергией между 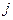 -ыми и
-ыми и 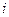 -ой фазами.
-ой фазами.
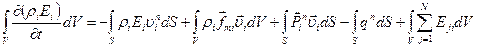 .
.
Аналогично (3.37) получается дифференциальное уравнение баланса полной энергии для 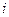 -ой фазы
-ой фазы 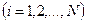 .
.
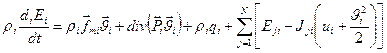 .
.
Модели энергетического взаимодействия фаз 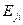 рассматриваются в специальной литературе.
рассматриваются в специальной литературе.

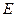 равна сумме удельных внутренних и кинетической энергии
равна сумме удельных внутренних и кинетической энергии 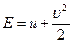 . Закон сохранения полной энергии является обобщением первого начала термодинамики для движения сплошных сред и формулируется следующим образом: индивидуальная производная по времени от полной энергии массы среды, содержащейся в движущемся объеме
. Закон сохранения полной энергии является обобщением первого начала термодинамики для движения сплошных сред и формулируется следующим образом: индивидуальная производная по времени от полной энергии массы среды, содержащейся в движущемся объеме 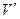 равна сумме мощностей, приложенных к выделенному объему и его поверхности внешних массовых и поверхностных сил и отнесенного к единице времени количества тепловой и немеханических видов энергии, подведенной извне к данной массе. Этот закон выражается в следующей интегральной форме:
равна сумме мощностей, приложенных к выделенному объему и его поверхности внешних массовых и поверхностных сил и отнесенного к единице времени количества тепловой и немеханических видов энергии, подведенной извне к данной массе. Этот закон выражается в следующей интегральной форме: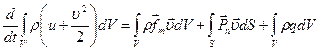 (3.30)
(3.30)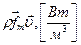 – удельная мощность объемных сил;
– удельная мощность объемных сил;  – удельная мощность поверхностных сил;
– удельная мощность поверхностных сил; 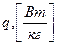 – удельная, отнесенная к единице массы тепловая и иные немеханические виды мощности подведенные извне.
– удельная, отнесенная к единице массы тепловая и иные немеханические виды мощности подведенные извне.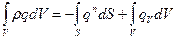 (3.31)
(3.31)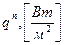 – удельная, отнесенная к единице площади поверхности, тепловая мощность;
– удельная, отнесенная к единице площади поверхности, тепловая мощность; 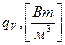 – удельная мощность объемных немеханических источников энергии.
– удельная мощность объемных немеханических источников энергии.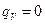 и уравнение (3.30) записывают в виде:
и уравнение (3.30) записывают в виде: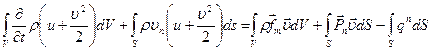 (3.32)
(3.32)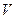 . Полагают, что в пределах КО параметры изменяются линейно или экспоненциально по пространственным координатам и времени. Производные заменяются отношением приращения функций к приращениям аргументов, например:
. Полагают, что в пределах КО параметры изменяются линейно или экспоненциально по пространственным координатам и времени. Производные заменяются отношением приращения функций к приращениям аргументов, например: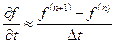 ,
, 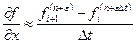 , (3.33)
, (3.33)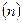 ,
, 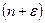 ,
, 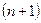 соответствуют моментам времени
соответствуют моментам времени 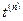 ,
,  ,
, 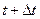 соответственно,
соответственно, 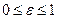 , значениям соответствуют неявные схемы,
, значениям соответствуют неявные схемы,  – явная схема. Интегралы заменяются произведениями средних значений по площади
– явная схема. Интегралы заменяются произведениями средних значений по площади 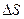 или объему
или объему 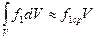 ,
, 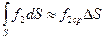 . (3.34)
. (3.34)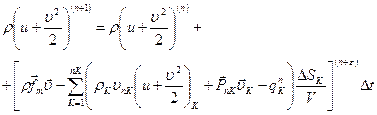 , (3.35)
, (3.35)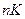 – число граней контрольного объема,
– число граней контрольного объема, 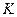 – номер грани.
– номер грани.
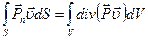
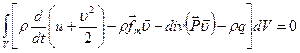 . (3.36)
. (3.36)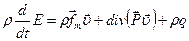 (3.37)
(3.37) (где N – число фаз в интегральной форме) для
(где N – число фаз в интегральной форме) для 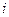 -ой фазы аналогично (3.32), однако включает в себя слагаемое
-ой фазы аналогично (3.32), однако включает в себя слагаемое 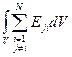 , которое характеризуется интенсивностью обмена энергией между
, которое характеризуется интенсивностью обмена энергией между 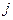 -ыми и
-ыми и 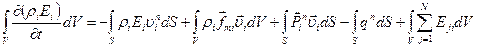 .
.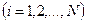 .
.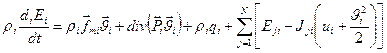 .
.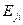 рассматриваются в специальной литературе.
рассматриваются в специальной литературе.


