Уравнение обращенного воздействия
В качестве исходной системы уравнений примем уравнения баланса массы, импульса и полной энтальпии § Уравнение баланса массы (расхода)
§ Уравнение движения
§ Уравнение баланса энтальпии
§ Уравнение состояния совершенного газа
Из уравнения (7.3) выразим Откуда, вводя
Выразим
где
Величина
Тогда Приравняв и, следовательно:
В частном случае при
Уравнение (7.8) называют уравнением обращенного воздействия.
|

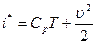 , а также уравнения состояния. Полагаем равным нулю тепловой поток от объемных источников тепла. Течение считаем установившемся. Тогда получим:
, а также уравнения состояния. Полагаем равным нулю тепловой поток от объемных источников тепла. Течение считаем установившемся. Тогда получим: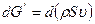 или
или  (7.1)
(7.1) (7.2)
(7.2)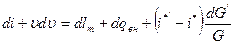 (7.3)
(7.3) или
или  (7.4)
(7.4) , с учетом
, с учетом  ,
, 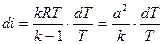 ;
; 
 - число Маха:
- число Маха: (7.5)
(7.5) ;
; 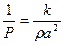 ;
;  . Из (7.4):
. Из (7.4): ,
, выразим из (7.2)
выразим из (7.2)
 найдем из (7.1)
найдем из (7.1)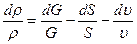
 , (7.6).
, (7.6).

 (7.7)
(7.7) ,
,  получаем уравнение
получаем уравнение (7.8)
(7.8)


