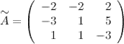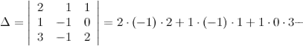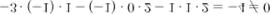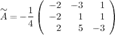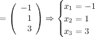Запишем заданную систему в матричном виде:
Если матрица  невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу
невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу  . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу
. Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу 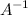 слева:
слева:

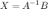
Поэтому, чтобы найти неизвестную матрицу 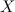 надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Данный метод удобно применять тогда, когда нужно решить много одинаковых систем с разными правыми частями.
Пример
Задание. Найти решение СЛАУ  матричным методом.
матричным методом.
Решение. Выпишем матрицу системы 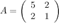 и матрицу правых частей
и матрицу правых частей  . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю:
. Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю:  ; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что
; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что
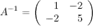
Тогда 
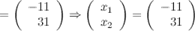
Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что  ,
, 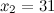
Пример

Решение. Запишем данную систему в матричной форме:
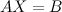 ,
,
где 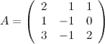 - матрица системы,
- матрица системы,  - столбец неизвестных,
- столбец неизвестных, 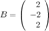 - столбец правых частей. Тогда
- столбец правых частей. Тогда
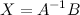
Найдем обратную матрицу 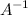 к матрице
к матрице 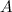 с помощью союзной матрицы:
с помощью союзной матрицы:
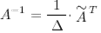
Здесь  - определитель матрицы
- определитель матрицы 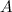 ; матрица
; матрица 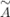 - союзная матрица, она получена из исходной матрицы
- союзная матрица, она получена из исходной матрицы 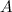 заменой ее элементов их алгебраическими дополнениями. Найдем
заменой ее элементов их алгебраическими дополнениями. Найдем 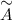 , для этого вычислим алгебраические к элементам матрицы
, для этого вычислим алгебраические к элементам матрицы 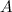 :
:
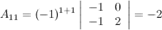
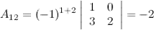
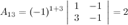
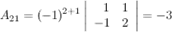
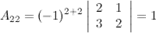


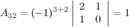
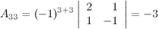 Таким образом,
Таким образом,
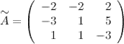
Определитель матрицы 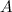
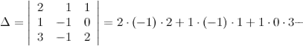
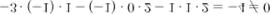
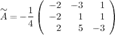
Отсюда искомая матрица

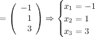

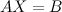
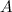 невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу
невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу 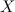 . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу
. Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу 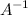 слева:
слева:
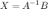
 матричным методом.
матричным методом.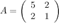 и матрицу правых частей
и матрицу правых частей  . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю:
. Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю:  ; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что
; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что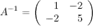

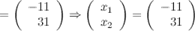
 ,
, 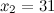

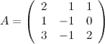 - матрица системы,
- матрица системы,  - столбец неизвестных,
- столбец неизвестных, 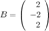 - столбец правых частей. Тогда
- столбец правых частей. Тогда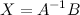
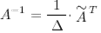
 - определитель матрицы
- определитель матрицы 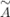 - союзная матрица, она получена из исходной матрицы
- союзная матрица, она получена из исходной матрицы 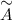 , для этого вычислим алгебраические к элементам матрицы
, для этого вычислим алгебраические к элементам матрицы 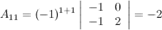
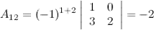
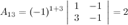
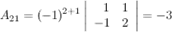
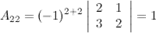


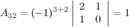
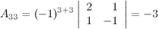 Таким образом,
Таким образом,