СЛАУ т. Кронекера-капеллиСистема уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Решением системы уравнений называется упорядоченный набор чисел - значений неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство. Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений Теорема Кронекера-Капелли. СЛАУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Задание. При каких значениях Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы
и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от первой строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:
Третью строку складываем с первой:
и меняем первую и вторую строки матрицы местами
Матрица приведена к ступенчатому виду. Получаем, что
|
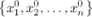называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
система 
будет совместной?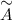
(слева от вертикальной черты находится матрица системы 
):
, 
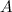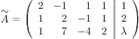
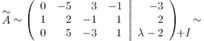
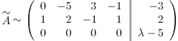
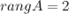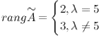. Таким образом, при 
система совместна, а при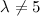 
- несовместна.
