Обратная матрица. Определение:Матрица называется обратной по отношению к квадратной матрице , если
Определение:Матрица
Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной. Так как Укажем следующие свойства обратных матриц: 1. (A-1)-1 = A; 2. (AB)-1 = B-1A-1 3. (AT)-1 = (A-1)T.
|

 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице  , если
, если .
. , то обратная матрица
, то обратная матрица 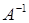 существует.
существует.


