Регресійний аналіз
Регресійний аналіз полягає в прогнозуванні однієї змінної на підставі іншої. Лінійний регресійний аналіз прогнозує значення однієї змінної на підставі іншої за допомогою прямої лінії. Нахил цієї лінії, виражається в одиницях вимірювання у на одну одиницю х і характеризує крутизну підйому або спуску (якщо b негативне) лінії. Зрушення, а, дорівнює значенню, яке приймає у при х, рівному 0. Лінія найменших квадратів характеризується найменшою зі всіх можливих ліній сумою зведених у квадрат помилок прогнозування по вертикалі й використовується як краща лінія прогнозування, заснована на даних. Нахил цієї лінії, b, називають також коефіцієнтом регресії у по х, а зрушення а (відрізок, що відсікається на осі у) називають також постійним членом регресії.
Прогнозоване значення для у при заданому значенні х визначається шляхом підстановки цього значення х в рівняння для лінії найменших квадратів. Кожна з точок даних характеризується залишком – помилкою прогнозування, яка вказує, наскільки вище або нижче за лінію знаходиться крапка. Існують дві міри відповідності лінії найменших квадратів наявним даним. Стандартна помилка оцінки,яку позначають Для обчислення:
Для інтерпретації:
Значення Довірчі інтервали й перевірка гіпотез для коефіцієнта регресії пов'язані з певними припущеннями щодо аналізованої сукупності даних, які повинні гарантувати, що вона складається з незалежних спостережень, що характеризуються лінійним взаємозв'язком із рівною варіацією та приблизно нормально розподіленою випадковістю. По-перше, ці дані повинні представляти собою довільну вибірку з тієї, що цікавить нас генеральній сукупності. По-друге, лінійна модель указує, що спостережуване значення у визначається взаємозв'язком у генеральній сукупності плюс випадкова помилка, що має нормальний розподіл. Існують параметри генеральної сукупності, що відповідають нахилу та зрушенню лінії найменших квадратів, побудованої на даних вибірки:
де
Статистичні висновки (використання довірчих інтервалів і перевірки статистичних гіпотез) щодо коефіцієнтів лінії найменших квадратів ґрунтуються, як завжди, на їх стандартних помилках і значеннях із Стандартна помилка коефіцієнта нахилу,
Стандартна помилка зрушення,
Довірчий інтервал для нахилу в генеральній сукупності β:
Довірчий інтервал для зрушення в генеральній сукупності α;:
Один із способів перевірки, чи є виявлений взаємозв'язок між х і у реальним або це просто випадковий збіг, полягає в порівнянні β з заданим значенням β0 = 0. Про значущий зв'язок можна говорити в тому випадку, якщо 0 не потрапляє в довірчий інтервал, що базується на b і Sb, або якщо абсолютне значення t = b/ Sb перевершує відповідне t- значенняв t- таблиці. Ця перевірка еквівалентна перевірці значущості коефіцієнта кореляції й означає, по суті, те ж саме, що і F- тестдля випадку, коли рівняння містить тільки одну змінну х. Зрозуміло, будь-який із коефіцієнтів (а або b ) можна порівняти з будь-яким відповідним заданим значенням, скориставшись одно - або двосторонньою перевіркою (залежно від конкретних обставин) і з використанням тих же методів перевірки, що були розглянуті для середнього генеральній сукупності. Для прогнозування середнього значення нового спостереження у за умови, що х = х0, невизначеність прогнозу оцінюють за допомогою стандартної помилки
Довірчий інтервал для прогнозованого (середнього) значення у при заданому значенні х0 має наступний вигляд: від
|

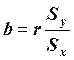 (10.7)
(10.7) (10.8)
(10.8) , приблизно указує величину помилок прогнозування (залишків) для наявних даних в тих же одиницях, в яких виміряна й змінна у. Відповідні формули приведені нижче.
, приблизно указує величину помилок прогнозування (залишків) для наявних даних в тих же одиницях, в яких виміряна й змінна у. Відповідні формули приведені нижче. (10.9)
(10.9) (10.10)
(10.10) , що називається коефіцієнтом детермінації,говорить про те, який відсоток варіації у пояснюється поведінкою х.
, що називається коефіцієнтом детермінації,говорить про те, який відсоток варіації у пояснюється поведінкою х. (10.11)
(10.11)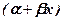 – взаємозв'язок у генеральній сукупності;
– взаємозв'язок у генеральній сукупності;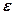 – випадковість, яка має нормальний розподіл з середнім значенням, що дорівнює 0, і постійним стандартним відхиленням
– випадковість, яка має нормальний розподіл з середнім значенням, що дорівнює 0, і постійним стандартним відхиленням 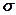 .
. , указує приблизну величину відхилення оцінки нахилу, b (коефіцієнт регресії, обчислений на основі даних вибірки), від нахилу в генеральній сукупності, β;, викликаного випадковим характером вибірки.
, указує приблизну величину відхилення оцінки нахилу, b (коефіцієнт регресії, обчислений на основі даних вибірки), від нахилу в генеральній сукупності, β;, викликаного випадковим характером вибірки. (10.12)
(10.12)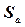 , указує приблизно, наскільки далеко оцінка зрушення а відстоїть від істинного зрушення α; у генеральній сукупності.
, указує приблизно, наскільки далеко оцінка зрушення а відстоїть від істинного зрушення α; у генеральній сукупності. (10.13)
(10.13) . (10.14)
. (10.14) . (10.15)
. (10.15)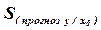 , яка також має п, – 2 ступенів свободи. Це дозволяє побудувати довірчі інтервали й перевірити гіпотези для нового спостереження:
, яка також має п, – 2 ступенів свободи. Це дозволяє побудувати довірчі інтервали й перевірити гіпотези для нового спостереження: (10.16)
(10.16) до
до 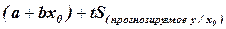 . (10.17)
. (10.17) Питання для самоконтролю
Питання для самоконтролю


