Види взаємозв'язків
Тема 10. статистичнІ методи аналізу кореляційних зв'язків План 10.1. Види взаємозв'язків Метод найменших квадратів Вимірювання тісноти зв'язку Регресійний аналіз Питання для самоконтролю Література Види взаємозв'язків Більшість економічних явищ має імовірнісний або випадковий характер, тобто, у реальних умовах дуже важко зі 100% упевненістю передбачати розвиток того або іншого економічного об'єкту. Природно, це факт приводить до деяких ускладнень, і вимагає наявність в управлінського персоналу сучасних підприємств навиків в області прогнозу невизначеного майбутнього – навиків екстраполювання. Екстраполяціязводиться до виявлення закономірностей, прихованих серед випадковостей минулого та сьогодення періодів, і перенесення цих закономірностей на майбутнє. Як правило, дослідження випадкових (кореляційних) взаємин зводиться до адаптації реальних імовірнісних взаємозв'язків до логіки функціональних залежностей, тобто іншими словами, потрібно визначити й аналітично виразити («проявити») форму передбачуваної залежності та потім досліджувати її. При дослідженні соціально-економічних явищ часто доводиться мати справу з взаємопов'язаними показниками. При чому часто зв'язок, який існує між двома або декількома показниками, затушовується, ускладнюється нашаруванням дії інших причин (чинників). Вивчити, наскільки зміна одного показника пов'язана зі зміною іншого (або декількох), – одне з найважливіших завдань статистики. Ознаки, які характеризують причини й умови зв'язку називають факторними ( Слід відрізняти функціональні й кореляційні зв'язки. При функціональному зв'язку кожному значенню змінної Прикладом кореляційного зв'язку може служити залежність продуктивності праці від стажу роботи працівників, залежність урожайності від терміну сівби, залежність проданих на біржі нерухомості однокімнатних квартир від їх вартості й розміру загальної площі. Найбільш простим випадком кореляційної залежності є парна кореляція, тобто зв'язок між двома ознаками (результативним і одним факторним). Основними завданнями при вивченні кореляційних залежностей є: 1) відшукування математичної формули, яка б відображала залежність 2) вимірювання тісноти зв'язку. Визначення форми зв'язку з наступним відшукуванням параметрів рівняння, називається знаходженням рівняння зв'язку (рівняння регресії). Рівняння регресії записується Залежно від характеру зв'язки використовують: лінійні рівняння (прямолінійний зв'язок): коли зі зміною нелінійні рівняння (криволінійний зв'язок), коли зміна взаємопов'язаних ознак відбувається нерівномірно (зі прискоренням, уповільненням або зі змінним напрямом зв'язку): параболічне, гіперболічне, і т. п. Параметри для всіх рівнянь визначають із системи нормальних рівнянь, яка будується за допомогою методу найменших квадратів (МНК).
|

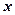 ), а ті, які характеризують наслідки зв'язку, – результативними (
), а ті, які характеризують наслідки зв'язку, – результативними (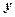 ).
).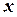 відповідає одне чітко певне значення
відповідає одне чітко певне значення 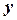 . Цей зв'язок виявляється однозначно в кожному окремому випадку. Зв'язок, при якому одному значенню змінної
. Цей зв'язок виявляється однозначно в кожному окремому випадку. Зв'язок, при якому одному значенню змінної 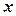 може відповідати (унаслідок нашарування дії інших причин) безліч значень іншої змінної,
може відповідати (унаслідок нашарування дії інших причин) безліч значень іншої змінної,  називають кореляційним (при зміні
називають кореляційним (при зміні 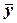 ). Кореляційний зв'язок виявляється тільки на основі масового спостереження.
). Кореляційний зв'язок виявляється тільки на основі масового спостереження.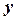 від
від  (читається: „ігрек, вирівняний по ікс”).
(читається: „ігрек, вирівняний по ікс”).


