Метод найменших квадратів
Суть методу найменших квадратів полягає в відшуканні параметрів моделі тренда, яка краще всього описує тенденцію розвитку якого-небудь випадкового явища в часі або в просторі (тренд – це лінія, яка й характеризує тенденцію цього розвитку). Завдання методу найменших квадратів (МНК) зводиться до знаходження не просто якоїсь моделі тренда, а до знаходження кращої або оптимальної моделі. Ця модель буде оптимальною, якщо сума квадратичних відхилень між спостережуваними фактичними величинами й відповідними їм розрахунковими величинами тренда буде мінімальною (найменшою):
де
МНК самостійно застосовується досить рідко. Як правило, частіше за всього його використовують лише як необхідний технічний прийом при кореляційних дослідженнях. Слід пам'ятати, що інформаційною основою МНК може бути тільки достовірний статистичний ряд, причому число спостережень не повинне бути менше 4-х, згладжуючі процедури МНК можуть бути помилковими. Інструментарій МНК зводиться до наступних процедур: Перша процедура. З'ясовується, чи існує взагалі яка-небудь тенденція зміни результативної ознаки при зміні вибраного чинника-аргументу, або іншими словами, чи є зв'язок між «у» і « Друга процедура. Визначається, яка лінія (траєкторія) здатна краще всього описати або охарактеризувати цю тенденцію. Третя процедура. Розраховуються параметри регресійного рівняння, що характеризує дану лінію, або іншими словами, визначається аналітична формула, що описує кращу модель тренда. Приклад. Припустимо, ми маємо інформацію про середню врожайність соняшнику в досліджуваному господарстві (табл. 10.1). Таблиця 10.1
Оскільки рівень технології при виробництві соняшнику в наший країні за останні 10 років практично не змінився, значить, коливання врожайності в аналізований період дуже сильно залежали від змін погодно-кліматичних умов. Чи дійсно це так? Перша процедура МНК. Перевіряється гіпотеза про існування тенденції зміни врожайності соняшнику залежно від зміни погодно-кліматичних умов за аналізованих 10 років. У даному прикладі за «y» доцільно прийняти врожайність соняшнику, а за «x» – номер спостережуваного року в аналізованому періоді. Перевірку гіпотези про існування якого-небудь взаємозв'язку між «
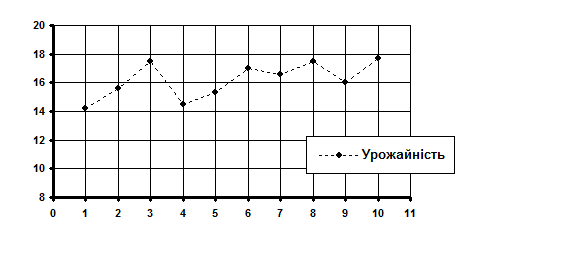
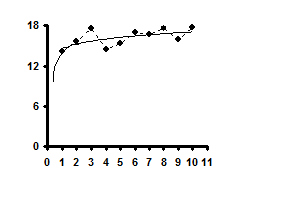
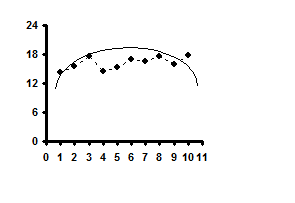
Кореляційне поле в нашому прикладі розташоване навколо повільно зростаючої лінії. Це вже само по собі говорить про існування певної тенденції в зміні врожайності соняшнику. Не можна говорити про наявність якої-небудь тенденції лише тоді, коли кореляційне поле схоже на круг, коло, строго вертикальна або строго горизонтальна хмара, або ж складається з хаотично розкиданих крапок. У решті всіх випадків слід підтвердити гіпотезу про існування взаємозв'язку між « Друга процедура МНК. Визначається, яка лінія (траєкторія) здатна краще всього описати або охарактеризувати тенденцію зміни врожайності соняшнику за аналізований період. За наявності комп'ютерної техніки підбір оптимального тренда відбувається автоматично. При «ручній» обробці вибір оптимальної функції здійснюється, як правило, візуальним способом – по розташуванню кореляційного поля. Тобто, з вигляду графіка підбирається рівняння лінії, яка краще за все підходить до емпіричного тренду (до фактичної траєкторії). Як відомо, у природі існує величезна різноманітність функціональних залежностей, тому візуальним способом проаналізувати навіть незначну їх частину - украй скрутно. На щастя, у реальній економічній практиці більшість взаємозв'язків достатньо точно можуть бути описані або параболою, або гіперболою, або ж прямою лінією. У зв'язку з цим, при «ручному» варіанті підбору кращої функції, можна обмежитися тільки цими трьома моделями.
Парабола другого порядку:
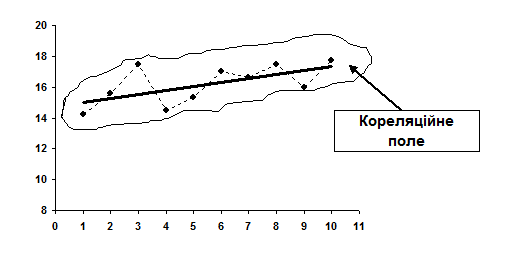
Неважко помітити, що в нашому прикладі краще всього тенденцію зміни врожайності соняшнику за аналізованих 10 років характеризує пряма лінія, тому рівнянням регресії буде рівняння прямої. Третя процедура. Розраховуються параметри регресійного рівняння, що характеризує дану лінію, або іншими словами, визначається аналітична формула, що описує кращу модель тренда. Знаходження значень параметрів рівняння регресії, у нашому випадку параметрів
Ця система рівнянь досить легко вирішується методом Гауса. Нагадаємо, що в результаті рішення, у нашому прикладі, знаходяться значення параметрів У лінійному рівнянні параметр Приведемо також системи нормальних рівнянь для відшукування параметрів нелінійних рівнянь. Таблиця 10.2
Слід пам'ятати, що при зміні хоч би одного значення вхідних даних (пари значень
|

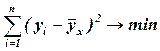 (10.1)
(10.1) - квадратичне відхилення між спостережуваною фактичною величиною та відповідною їй розрахунковою величиною тренда;
- квадратичне відхилення між спостережуваною фактичною величиною та відповідною їй розрахунковою величиною тренда;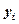 - фактичне (спостережуване) значення явища, що вивчається;
- фактичне (спостережуване) значення явища, що вивчається;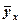 - розрахункове значення моделі тренда;
- розрахункове значення моделі тренда;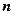 - число спостережень за явищем, що вивчається.
- число спостережень за явищем, що вивчається.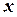 ».
».
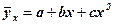 :
:
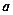 і
і 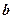 , є серцевиною МНК. Даний процес зводиться до вирішення системи нормальних рівнянь.
, є серцевиною МНК. Даний процес зводиться до вирішення системи нормальних рівнянь.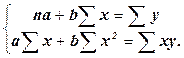 (10.2)
(10.2) і
і 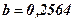 . Таким чином, знайдене рівняння регресії матиме наступний вигляд:
. Таким чином, знайдене рівняння регресії матиме наступний вигляд: 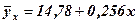
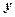 із зміною
із зміною 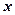 на одиницю. Він має одиницю вимірювання результативної ознаки. У разі прямого зв'язку
на одиницю. Він має одиницю вимірювання результативної ознаки. У разі прямого зв'язку 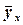 при
при 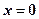 . Якщо
. Якщо 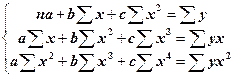
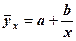
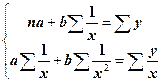
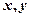 або одного з них) усі коефіцієнти змінять у загальному випадку свої значення, тому що вони повністю визначаються вхідними даними. Тому при повторній апроксимації з декількома зміненими даними буде отримана інша апроксимуюча функція з іншими коефіцієнтами.
або одного з них) усі коефіцієнти змінять у загальному випадку свої значення, тому що вони повністю визначаються вхідними даними. Тому при повторній апроксимації з декількома зміненими даними буде отримана інша апроксимуюча функція з іншими коефіцієнтами.


